Pression de radiation
Partie
Question
On considère une onde électromagnétique, non-nécessairement plane, ayant une densité d'énergie \(w\). Sa vitesse de propagation dans le milieu considéré (\(\varepsilon, \mu\)) est \(c\).
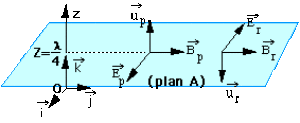
On considère les surfaces \(A\) et \(A'\), orthogonales à un axe noté \(z\) (de vecteur unitaire \(\vec u\)), et un élément de volume \(\tau\) cylindrique, de longueur \(dz\), s'appuyant sur ces surfaces : \(A\) (située en \(z\)) et \(A'\) (en \(z - dz\)).
La normale à la surface \(A\) considérée, dirigée vers l'extérieur du volume, est de même sens que \(\vec u\) (faire un schéma). Deux cas seront envisagés :
Cas 1 : l'onde est progressive dans le sens de \(\vec u\)).
Cas 2 : l'onde est stationnaire dans la direction définie par l'axe \(z\).
a- Dans chacun de ces 2 cas :
Montrer que la force de radiation sur la surface \(A\) considérée s'exprime \(\vec{F_{rad}}= A.w.\vec u\) (la pression de radiation est donc dans les 2 cas : \(p_{rad} = w\)).
b- On précise maintenant la forme des ondes considérées :
Cas 1 : l'onde progressive est : \(\left|\begin{array}{l} \vec{E_p}=\vec i.E_0.\cos(\omega t-Kz) \\ \vec{B_p}=\vec j.(\frac{E_0 }{c}).\cos(\omega t-Kz) \end{array} \right.\)
Cas 2 : l'onde stationnaire est : \(\left|\begin{array}{l} \vec E=\vec i.2E_0.\cos\omega t.\cos Kz \\ \vec B=\vec j.(\frac{2E_0 }{c}).\sin\omega t.\sin Kz \end{array} \right.\)
Déduire de la question a- les expressions de \(p_{rad }\).
Montrer que ces ondes sont planes.
Vérifier que l'onde stationnaire peut s'obtenir par superposition de l'onde progressive et d'une onde régressive dont les champs \(\vec{E_r}\) et \(\vec{B_r}\) ont respectivement même amplitude que \(\vec{E_p}\) et \(\vec{B_p}\).
Préciser à quelle côte \(z\) sera située la surface \(A\) pour pouvoir satisfaire la condition de réflexion (de \(\vec E\)), telle que cette réflexion de l'onde progressive considérée dans le cas 1, produise l'onde stationnaire du cas 2.
En utilisant la valeur de \(K_z\) correspondant à cette condition de réflexion, donner alors dans les cas 1 et 2 les expressions de \(w\).
c- On considère l'onde plane stationnaire précédente.
Exprimer son Vecteur de Poynting sur la surface \(A\) définie par : \(\cos K_{z_A }= 0\).
Exprimer son Vecteur de Poynting sur la surface \(A'\) située à la côte \(z_{A'} (z_A - z_{A'} = \delta z)\).
Montrer que si \(\delta z\simeq0\), la composante sur \(z\) de ce vecteur peut se mettre sous la forme \(S_z (\delta z) \simeq 4c \varepsilon E_0^2. \sin\omega t. \cos\omega t. K.\delta z\)
Exprimer le flux du Vecteur de Poynting à travers la surface \(S\) fermée qui délimite le volume \(\tau\) défini précédemment.
En déduire l'expression de \(\frac{\partial w_{st}}{\partial t}\) (où \(w_{st}\) est la densité d'énergie de l'onde stationnaire).
NB : Remarquer que cette dérivée ne dépend que de la variable \(t\), d'où l'on peut déduire que : \(\frac{\partial w_{st}}{\partial t}=\frac{dw_{st}}{dt}\)
Par intégration de cette dernière expression, montrer que : \(p_{rad}= w_{st} = 2\epsilon E_0^2. sin^2\omega t\)
Vérifier que cette valeur de \(w_{st}\) est bien celle que l'on trouve directement en appliquant la relation générale entre \(w\) et le carré des champs \(\vec E\) et \(\vec B\). (Ne pas oublier que l'on calcule la valeur de \(w_{st}\) sur la surface \(A\) telle que : \(cos K_{z_A} = 0\)).
d- Synthèse.
De la même façon qu'en c- et sur cette même surface \(A\), calculer directement la densité d'énergie \(w_p\). de l'onde progressive. En déduire celle \(w_r\) de l'onde régressive correspondante.
Vérifier que \(w_{st}= w_p+ w_r = 2.w_p\).
Commenter ce résultat en se référant au tableau du Cours. Après avoir fait les deux derniers exercices : compléter ce tableau.
e- Stabilité des poussières interstellaires.
L'intensité du rayonnement solaire est donnée en fonction de la distance \(R\) au soleil par la relation \(I=\frac{P}{4\pi R^2}\) et la force de gravitation sur une masse \(m\) est donnée par : \(F_g=\frac{GM_s.m}{R^2}\).
Cette intensité est de \(\textrm{1,4 kW/m}^2\) à la distance \(R=\textrm{1,5.10}^{11}\textrm m\).
Comparer la force exercée par le rayonnement solaire sur une particule absorbante de poussière de diamètre \(10^{-6} \textrm{ m}\) et de densité \(\textrm{3.10}^3\textrm{ kg/m}^3\) avec celle de l'attraction solaire, lorsque la particule est distante du soleil de \(R\).
On donne : la masse du soleil \(M_s=2.10^{30} \textrm{ kg}\)
et la constante d'attraction universelle \(G= \textrm{6,67 10}^{-11} \textrm{ N.m}^2\textrm{/kg}^2\).
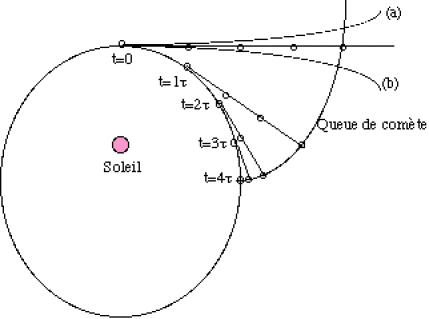
La poussière relâchée par une comète ne suit pas la trajectoire de celle- ci à cause de la pression de radiation, ce qui permet d'exprimer la forme de celle-ci.
Supposons que les particules de poussière soient de rayon \(r\), de densité \(\rho = \textrm{3,5 10}^3 \textrm{kg/m}^3\) et quelles absorbent complètement la lumière solaire.
Pour quelle valeur de \(r\) la force de gravitation due au soleil s'équilibre avec celle due à la pression de radiation.
On montrera que ce résultat est indépendant de la position de la poussière par rapport au soleil.
On se propose de reconstituer approximativement la forme de la queue de la comète.
On suppose que le noyau de la comète suit une trajectoire elliptique autour du soleil (voir figure ci-après) et on considère les poussières qui ont un rayon \(r\) calculé à la question précédente.
On admet qu'une poussière n'est soumise qu'à l'attraction solaire et à la force de radiation du soleil. Dans ces conditions :
Quelle est la nature de la trajectoire d'une poussière après son abandon par le noyau de la comète ?
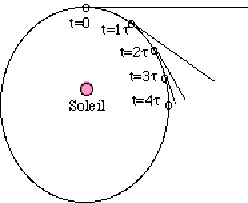
On considère les poussières lâchées successivement aux instants \(t = 0, 1\tau, 2\tau\) et \(3\tau\) . Le noyau de la comète se trouve aux points successifs indiqués sur l'ellipse ci-dessus. Dessiner les positions, à l'instant \(4\tau\), des particules qui ont été relâchées aux instant \(0, 1\tau, 2\tau\) et \(3\tau\).L'ensemble de ces positions donne l'allure de la queue de poussière de la comète.
À partir de l'instant \(t = 0\), indiquer qualitativement les trajectoires pour des particules de même masse mais ayant un rayon :
supérieur à \(r\)
inférieur à \(r\).
Aide simple
Revoir la structure d'onde électromagnétique plane (qui permet d'exprimer le champ magnétique en fonction du champ électrique) et la définition du vecteur de Poynting.
Solution détaillée
a- Force de radiation
On veut connaitre la force de radiation exercée sur la surface \(A\) dans les deux cas :
onde progressive (se propageant dans le sens de \(z\))
onde stationnaire (dans la direction définie par \(z\)).
Ces deux cas peuvent se réaliser en considérant une onde progressive qui arrive sur une cible A.
Soit l'énergie est totalement absorbée par la cible. Alors, il n'y a pas d'onde réfléchie par la cible.
Soit l'énergie n'est pas du tout absorbée par la cible et l'onde progressive est réfléchie par la cible.
Dans ce dernier cas, la superposition de l'onde progressive et de l'onde régressive donne une onde stationnaire.
Le problème posé peut donc se résoudre strictement en reprenant les arguments du cours. On trouve dans ces conditions :
Absorption d'énergie sans réflexion (onde progressive seule) \(\Rightarrow p_{rad}=w\)
Réflexion sans absorption d'énergie (onde progressive+régressive) \(\Rightarrow p_{rad}=2w\).
Dans les 2 cas, \(w\) désigne la densité d'énergie de l'onde progressive sur la surface \(A\).
Comme dans le second cas il n'y a pas d'absorption d'énergie par la cible \(A\), la densité d'énergie sur A de l'onde réfléchie est la même que la densité d'énergie de l'onde incidente. Avec les conditions particulières de réflexion définies sur la cible, \(2w\) représente alors la densité d'énergie totale de l'onde stationnaire.
Autrement dit, avec ces conditions de réflexion, si l'on note \(w\) la densité d'énergie de l'onde (progressive ou stationnaire), la pression de radiation est \(p_{rad}= w\).
Noter que, dans tous les cas, la densité d'énergie est une variable locale c'est-à dire définie en un point (ou dans un domaine élémentaire, ou ici, en tous les points d'une surface élémentaire \(A\)).
On va maintenant calculer directement la pression de radiation.
On considère une surface cylindrique fermée \(S\) de surface de base \(A\) et d'épaisseur \(\delta z = c \delta t\) (\(c\) vitesse de l'onde électromagnétique dans le vide). Le volume contenu dans \(S\) est donc : \(A.\delta z\)
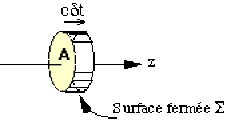
Dans ce volume, la densité d'énergie est \(w\), l'énergie est donc : \(\delta w = w.A . \delta z = w .A.c.\delta t\)
\(\Rightarrow \frac{\delta w}{\delta t}=A.c.w\)
On note \(\vec P\) la quantité de mouvement de l'onde électromagnétique \(\Rightarrow w=c.P\)
\(\Rightarrow A.cw=c\frac{\delta P}{\delta t} \Rightarrow A.w=\frac{\delta P}{\delta t}\rightarrow\frac{dP}{dt}\) quand \(\delta t\rightarrow0\)
Par définition, la force (ici force de radiation) est toujours : \(\vec F=\frac{\vec{dP}}{dt}\)
\(F=\frac{dP}{dt}\Rightarrow F=A.p_{rad}\Rightarrow p_{rad}=\frac{F}{A}=w\), où \(w\) est la densité d'énergie totale de l'onde électromagnétique en \(A\).
b- Onde progressive, onde stationnaire.
La densité d'énergie de l'onde électromagnétique est toujours : \(w=\frac{\varepsilon E^2}{2}+\frac{B^2}{2\mu}\)
On doit utiliser les expressions qui définissent \(\vec E\) et \(\vec B\) pour calculer \(w\).
b-1
Cas 1 Pour l'onde progressive définie par : \(\vec{E_p}=\vec iE_0\cos(\omega t-Kz)\) et
\(\vec{B_p}=\vec j\frac{E_0}{c}\cos(\omega t-Kz)\) la densité d'énergie est définie en tout point \(z\) et à tout instant \(t\) par :
\(w_p=\frac{\varepsilon}{2}E_0^2\cos^2(\omega t-Kz)+\frac{E_0^2}{2\mu c^2}(\cos^2\omega t-Kz)= \frac{\varepsilon}{2}E_0^2\cos^2(\omega t-Kz)[1+\frac{1}{\varepsilon\mu c^2}]\)
\(\frac{1}{\varepsilon\mu c^2}=1\Rightarrow w_p=\varepsilon E_0^2\cos^2(\omega t-Kz)\) en tout point \(z\) et à tout instant \(t\).
Cas 2 Pour l'onde stationnaire particulière : \(\vec E=\vec i2E_0\cos\omega t.\cos Kz\)
et \(\vec B=\vec j2\frac{E_0}{2}.\sin\omega t.\sin Kz\)
la densité d'énergie est alors définie en tout point \(z\) et à tout instant \(t\) par :
\(w_{sta}=\frac{\varepsilon}{2}4E_0^2\cos^2\omega t.\cos^2Kz+\frac{1}{2\mu}\frac{4E_0^2}{c^2}\sin^2\omega t .\sin^2Kz\)
\(w_{sta}=2\varepsilon E_0^2(\cos^2\omega t.\cos^2Kz+\sin^2\omega t.\sin^2Kz)\)
b-2
Ces ondes sont planes car ne dépendent que d'une seule variable d'espace (\(z\)) : l'onde progressive et l'onde stationnaire sont invariantes dans tout plan orthogonal à \(\vec k\).
b-3
L'onde stationnaire qui est donnée ici s'obtient par superposition de l'onde progressive et d'une onde régressive. En effet, si on connait :
\(\vec{E_p}=\vec iE_0\cos(\omega t-Kz)\) et \(\vec{E_p}+\vec{E_r}=\vec E=\vec i2E_0\cos\omega t.\cos Kz\)
\(\vec{B_p}=\vec j\frac{E_0}{c}\cos(\omega t-Kz)\) et \(\vec{B_p}+\vec{B_r}=\vec B=\vec j2\frac{E_0}{c}\sin\omega t.\sin Kz\)
alors, l'onde régressive doit être de la forme :
\(\vec{E_r}=\vec iE_0\cos(\omega t+Kz)\) \(\vec{B_r}=-\vec j\frac{E_0 }{c} \cos(\omega t+Kz)\)
(se rappeler que : \(\cos p+\cos q=2cos\frac{p+q}{2}.\cos\frac{p-q}{2}\)
et \(\cos p-\cos q=-2\sin\frac{p+q}{2}.\sin\frac{p-q}{2}\))
b-4
Dans ces conditions, la cible A ( en \(Z = \frac{\lambda}{4}\)) est un nœud de vibration pour \(\vec E. (cos \frac{\pi}{2}= 0)\)
Remarque 1 : c'est la condition de réflexion sur la cible (\(\vec E= 0\)) qui permet de définir la forme de l'onde régressive qui prend naissance par la réflexion de l'onde progressive. La forme de l'onde progressive et de l'onde stationnaire étant données ici, on peut donc en déduire l'endroit où se produit la réflexion ainsi que la forme de l'onde régressive.
Remarque 2 : Les relations qui définissent les densités d'énergie en tout point \(z\) et à tout instant t sont respectivement : \(w_p=\varepsilon E_0^2\cos^2(\omega t-Kz)\) (progressive)
\(w_{sta}=2eE_0^2(\cos^2\omega t.\cos^2Kz+\sin^2\omega t.\sin^2Kz)\) (stationnaire)
donc : \(w_{sat}\neq2.w_p \)! ! !
b-5
Par contre localement, sur la surface de la cible A (en \(z=Z=\frac{\lambda}{4}),KZ=\frac{\pi}{2}\)
\(\begin{array}{l} \Rightarrow w_p=\varepsilon E_0^2\cos^2(\omega t-KZ)=\varepsilon E_0^2\sin^2(\omega t) \\ \textrm{ et } w_{sta}=2\varepsilon E_0^2(\cos^2\omega t.\cos^2KZ+\sin^2\omega t.\sin^2KZ)=2\varepsilon E_0^2\sin^2(\omega t) \end{array}\Rightarrow w_{sta}=2.w_p\)
On retrouve bien la relation démontrée dans le cours concernant la densité d'énergie sur la cible.
c- Densité d'énergie de l'onde stationnaire.
Pour toute onde électromagnétique, le vecteur de Poynting est : \(\vec S=\frac{1}{\mu}\vec E\land\vec B\)
Ici, le champ (stationnaire) a simplement pour composantes : \(E_x=2E_0\cos\omega t.\cos Kz\) \(B_y=2\frac{E_0}{c}\sin\omega t.\sin Kz\)
\(\Rightarrow \vec S=Sz.\vec k\) avec \(S_z=\frac{E_xB_y}{\mu_0}=\frac{4E_0^2}{\mu c}\sin\omega t.\cos\omega t.\sin Kz..\cos Kz\)
\(\varepsilon \mu c^2=1 Sz (z,t)=4 \varepsilon .cE_0^2\sin\omega t.\cos\omega t.\sin Kz.\cos Kz\)
c-1
Sur le miroir (en \(z=Z_A=\frac{\lambda}{4})\Rightarrow \cos KZ_A=0\) et \(\sin K Z_A=1\) (déjà vu) \(\Rightarrow Sz (Z_A,t)=0\)
Le vecteur de Poynting est nul sur la surface \(A\).
c-2
Sur la surface A' située à l'ordonnée \(Z_{A'}\) telle que : \(Z_A - Z_{A'} = \delta z\)
\(Sz(Z_{A'},t)=4 \varepsilon .cE_0^2\sin\omega t.\cos\omega t.\sin KZ_{A'}\cos KZ_{A'}\)
En remplaçant : \(KZ_{A'}=KZ_A-K \delta z\)
\(\Rightarrow\sin KZ_{A'}=\sin(KZ_A-K \delta z)=\sin KZ_A.\cos K \delta z-\cos KZ_A.\sin K \delta z\)
\(\Rightarrow\cos KZ_{A'}=\cos(KZ_A-K \delta z)=\cos KZ_A.\cos K \delta z-\sin KZ_A.\sin K \delta z\)
Faisant tendre \(\delta z\rightarrow0\Rightarrow\cos K \delta z\rightarrow1\) et \(\sin K \delta z\rightarrow K \delta z\)
\(\Rightarrow\sin KZ_{A'}\rightarrow\sin KZ_A=1\)
\(\Rightarrow\cos KZ_{A'}\rightarrow\cos KZ_A-\sin KZ_A.K \delta z=K \delta z\)
\(\Rightarrow S_z(Z_{A'},t)\rightarrow4\varepsilon .cE_0^2\sin\omega t.\cos\omega t . K \delta z\)
c-3
On a donc : \(S_z(Z_A,t)=0 \textrm{ et } S_z(Z_A+\delta z,t)=4\varepsilon .cE_0^2\sin\omega t.\cos\omega t.K \delta z\)
Considérant la surface fermée \(\Sigma\) définie précédemment : le flux du vecteur de Poynting à travers la surface latérale est nul, celui à travers la surface \(A\) (située en\( Z_A\)) est nul, il ne reste que celui à travers la surface \(A'\) située en \(Z_A + \delta z\). (revoir le schéma question a)
\(\Rightarrow \iint_{\Sigma}\vec S.\vec{d\Sigma}=\iint_{A'}S_z(Z_A+\delta z,t).dA'=-A'.4\varepsilon cE_0^2\sin\omega t.\cos \omega t.K\delta z\)
Par ailleurs, \(A'=A\) et \(A'.\delta z\) est le volume \(t\) contenu à l'intérieur de la surface \(\Sigma\).
\(\Rightarrow-\frac{\partial w}{\partial t}=\iint_{\Sigma}\vec S.\vec{d\Sigma}=-\tau4K\varepsilon cE_0^2 \sin\omega t\cos\omega t\)
Avec \(\frac{\partial w}{\partial t}=\tau\frac{\partial w}{\partial t}\Rightarrow\frac{\partial w}{\partial t}=4K \varepsilon cE_0^2\sin\omega t\cos\omega t\)
La densité d'énergie stationnaire ne dépend donc que du temps \(t\)
\(\Rightarrow\) on peut intégrer cette relation :
\(\frac{dw}{dt}=-4K\varepsilon cE_0^2\sin\omega t\cos\omega t\Rightarrow w=4\varepsilon cE_0^2\frac{K}{\omega} \int\sin\omega t\cos\omega t . d(\omega t)\)
En notant \(w_{sta}\) la densité d'énergie stationnaire \(\Rightarrow w_{sta}=2\varepsilon E_0^2\frac{Kc}{\omega}\sin^2\omega t\)
\(K=\frac{2\pi}{\lambda}\), \(\omega=\frac{2\pi}{T}\Rightarrow\frac{K}{\omega}=\frac{T}{\lambda}=\frac{T}{CT}=\frac{1}{C}\Rightarrow \frac{Kc}{\omega}=1\)
\(\Rightarrow w_{sta}=2\varepsilon E_0^2\sin^2\omega t\)
c-4
Cette relation est bien la relation attendue, puisqu'on a trouvé à la question -b.5-
\(w_{sta}=2\varepsilon E_0^2(\cos^2\omega t . \cos^2KZ+\sin^2\omega t . \sin^2KZ)\). En y reportant \(\cos^2KZ_A=0\)
et \(\sin^2KZ_A=1\), on a bien : \(w_{sta}=2\varepsilon E_0^2\sin^2\omega t\)
- d - Synthèse
d-1

d-2

e- Stabilité des poussières interstellaires
e-1- Calculons la pression de radiation exercée sur une poussière.
L'intensité \(I\) rayonnée par le soleil possède une symétrie sphérique (i.e. sur la surface d'une sphère de rayon \(R\) centrée sur le soleil).
\(I=\frac{P}{4 . \pi . R^2}\)
où la puissance \(P\) rayonnée est reliée à l'énergie \(\delta w\) rayonnée pendant le temps \(\delta t\) par la relation : \(P=\frac{\delta w}{\delta t}\). D'où, \(I=\frac{\delta w}{\delta t}\frac{1}{4 . \pi . R^2}\)
La quantité de mouvement de l'onde est : \(\vec p=\frac{w}{c}\vec u\)
La force de radiation s'exprime par la variation de quantité de mouvement.
Si la quantité de mouvement de l'onde est initialement \(\vec p\) puis \(\vec0\) après interaction avec la cible, la force de radiation est alors :
\(\vec F_{rad}=\frac{\delta\vec p}{\delta t}=\frac{\delta w}{\delta t}\frac{1}{c}\vec u=(4 . \pi . R^2)\frac{I}{c}\vec u\)
Dans ce cas, la quantité de mouvement de l'onde étant nulle après l'interaction, cela signifie que l'onde n'est pas réfléchie et que son énergie a été absorbée par la cible.
Si la quantité de mouvement de l'onde est initialement \(\vec p\) puis \(-\vec p\) après interaction avec la cible, cela signifie que l'onde a été réfléchie sans absorption d'énergie. On est ici dans cette situation : les particules réfléchissent la lumière ce qui les rend visibles depuis la Terre ; et on admettra simplement que les particules n'absorbent pas du tout l'énergie de l'onde.
Dans ce cas, la variation de quantité de mouvement de l'onde est donc le double de la précédente, soit : \(\vec F_{rad}=2 . (4 . \pi . R^2)\frac{I}{c}\vec u\)
Par définition, la pression de radiation est la force de radiation par unité de surface. À la distance \(R\), le soleil rayonne sur une surface (\(4 . \pi . R^2\)).
La pression de radiation de l'onde sur les particules est donc : \(p_{rad}=2\frac{I}{c}\)
Dans cette expression, \(I\) est l'énergie rayonnée par unité de surface par unité de temps et \(c\) la vitesse de la lumière. (\(I\) s'exprime en watt par seconde par \(m^2\)).
Vérification : équation aux dimensions.
\([W]=[F].[L]=[M].[L]^2.[T]^{-2}\) (watt)
\(I=[W].[L]^{-2}[T]^{-1}=[M][L]^2[T]^{-2}.[L]^{-2}[T]^{-1}=[M].[T]^{-3}\)
\(c=[L].[T]^{-1}\)
\([F(I,c)]=[M][T]^{-3}.[L]^{-1}.[T]=[M].[L]^{-1}.[T]^{-2}\)
Une force a pour dimension \([M].[L].[T]^{-2}\)
On peut vérifier la cohérence avec la relation : \(\vec F_{rad}=\frac{\delta\vec p}{\delta t}=\frac{\delta W}{\delta t}\frac{1}{c}\vec u=(4 . \pi . R^2) \frac{I}{c}\vec u\)
qui donne \([W/c]T^{-1}=[M.L.T^{-1}]T^{-1}=M.L.T^{-2}=F\)
La pression de radiation est une force par unité de surface
\(p_{rad}=[M].[L].[T]^{-2}[L]^{-2}=[M].[L]^{-1}.[T]^{-2}\)
\([ I / c ]\) a bien la dimension d'une pression (de radiation)
\(p_{rad}\) s'exprime en \(\textrm {Newton / m}^2\).
Calcul.
\(p_{rad}=2(\textrm{1,4 KW/s/m}^2)/(3.10^8 \textrm{ m/s})=2(\textrm{1,4.10}^3)/(3.10^8)[\textrm{W.s/(m.m}^2)]\)
\(=\textrm{2,8.10}^3.10^{-8}/3. \textrm{W.s/(m.m}^2)=\textrm{0,93.10}^{-5} \textrm{N/m}^2 \Rightarrow p_{rad}\approx10^{-5} \textrm{N/m}^2\)
La surface de la poussière perpendiculairement au rayonnement (maitre couple) étant \(S = \textrm{0,8 10}^{-12} \textrm{ m}^2\), la force exercée par la radiation solaire sur la poussière est donc :
\(F_{rad}=p_{rad}. S=10^{-5}.\textrm{0,8.10}^{-12}=\textrm{0,8.10}^{-17} \textrm N\).
La force de gravitation est : \(F_g=\frac{GM_sm}{R^2}\) avec \(m=\rho 4 \pi r^3/3=1,6.10^{-15} kg\)
\(F_g=\textrm{0,9.10}^{-17}\textrm N\).
Ces deux forces ont des valeurs très voisines. Cela explique que les poussières interplanétaires ne tombent pas sur le soleil.
e-2- Forme de la queue d'une comète.
L'intensité de la radiation solaire est donnée en fonction de la distance \(R\) au soleil par la relation :
\(I=\frac{P}{4 . \pi . R^2}\)
Dans cette expression, \(P\) est la puissance émise par le soleil soit \(P = \textrm{3,9 10}^{26}\) watt et \(4\pi R^2\) la surface de la sphère de rayon \(R\) centrée sur le soleil.
On a vu que la force liée à la radiation globale sur une sphère de rayon \(R\) est :
\(\vec{F}_{rad}=2(4 . \pi . R^2)\frac{I}{c}\vec u\)
\(\Rightarrow\) la pression de radiation sur la particule à la distance \(R\) est :
\(p_{rad} = 2. \frac{I}{c}\)
La force de radiation sur cette particule de rayon \(r\) est:
\(F_{rad}=p_{rad}(4 . \pi . r^2)=2\frac{I}{c}(4 . \pi . r^2)=2P\frac{r^2}{c . R^2}\)
La force de gravitation est : \(F_g=\frac{G . M_s . m}{R^2}=\frac{G . M_s . 4 . \pi . r^3 . \rho}{3 . R^2}\)
En égalant les forces : \(\frac{G.M_s.4.\pi. r^3.\rho}{3R^2}=2P\frac{r^2}{cR^2}\), il vient \(r=\frac{3P}{2 .\pi .\rho . c . G . M_s}\), relation qui est indépendante de la distance \(R\).
Pour une particule parfaitement réfléchissante, on trouve l'égalité des forces de gravitation et de radiation pour \(r\simeq\textrm{0,48.10}^{-7} \textrm{m\`etres}\).
(soit, un diamètre très proche de celui \(10^{-6}\) mètre indiqué question précédente).
La résultante des forces agissant sur ces particules est donc nulle.
Pour des particules ayant ce rayon \(r\), après abandon de la comète, leur trajectoire est donc rectiligne, avec une vitesse en module égale à celle de la comète.
Ainsi en portant, sur les tangentes à la trajectoire de la comète en supposant le module de la vitesse constant, les différentes positions des poussières pour les différents intervalles de temps t on obtient en rejoignant les points pour un même \(t\) la forme de la queue de la comète.
Pour des rayons inférieurs à \(r\), la force de radiation (en \(r^2\)) l'emporte sur celle de gravitation en \(r^3\) et la particule suit le chemin (a).
À contrario, pour des rayons supérieurs à \(r\), c'est la force de gravitation qui l'emporte et la particule suit le chemin (b).