Flux d'énergie - onde stationnaire
Partie
Question
On considère l'onde progressive : \(\vec{E_p}=\vec i.E_0.\cos(\omega t-Kz)\) et l'onde régressive : \(\vec{E_r}=\vec i.E_0.\cos(\omega t+Kz)\).
Exprimer les parties magnétiques correspondantes \(\vec{B_p}\) et \(\vec{B_r}\) de ces ondes électromagnétiques planes.
En déduire l'expression des champs \(\vec E\) et \(\vec B\) de l'onde stationnaire obtenue, sous la forme :
\(E_x=2E_0.\cos\omega t.\cos Kz \textrm{ et } B_y=\Big(\frac{2E_0}{c}\Big).\sin\omega t.\sin Kz\).
Les résultats de la question -4- de l'exercice précédent sont-ils valables dans ce cas? Justifier.
Peut-on exprimer la densité d'énergie électrique (resp. magnétique) comme somme des densités d'énergie électrique (resp. magnétique) des ondes progressive et régressive?
Exprimer les densités d'énergie électrique et d'énergie magnétique de l'onde stationnaire.
En déduire que les densités d'énergie électrique et magnétique :
ont des maxima successifs :
séparés dans le temps par \(\frac{T}{4}\) (où \(T\) est la période des oscillations)
séparés dans l'espace par \(\frac{\lambda}{4}\) (où \(\lambda\) est la longueur d'onde)
oscillent harmoniquement en quadrature et à une pulsation \(2\omega\) (double de la pulsation \(\omega\) du champ électromagnétique).
Exprimer la densité totale d'énergie et en déduire qu'elle oscille entre la forme électrique et la forme magnétique.
Exprimer le vecteur de Poynting de cette onde stationnaire.
Montrer que sa moyenne sur \(\frac{T}{2}\) est nulle.
Montrer que sa moyenne sur \(\frac{\lambda}{2}\) est nulle.
Commenter ces résultats.
Montrer que l'énergie totale est la somme d'une énergie é.m. progressive et d'une énergie é.m. régressive.
Aide simple
Revoir la structure d'onde électromagnétique plane (qui permet d'exprimer le champ magnétique en fonction du champ électrique) et la définition du vecteur de Poynting.
Rappel de cours
Voir la page Flux d'énergie dans une onde plane
Solution détaillée
1. Pour une onde électromagnétique plane se propageant dans le vide (à la vitesse \(c\)) selon le vecteur unitaire \(\vec u\), on a :
\(\vec B=\frac{1}{c}~\vec u\land\vec E\Leftrightarrow\vec E=-c~\vec u\land\vec B\)
Dans cet exercice, l'onde progressive se propage selon \(\vec k\) et l'onde régressive selon \(-\vec k\).
\(\begin{array}{lllll} \Rightarrow &\vec{E_p}&=&E_{pX}\vec i &\Rightarrow \vec{B_p}=\frac{E_{pX}}{c}\vec j=\cos(\omega t-Kz)\vec j\\ &\vec{E_r}&=&E_{rX}\vec i &\Rightarrow \vec{B_r}=\frac{E_{rX}}{c}(-\vec j)=-\frac{E_0}{c}\cos(\omega t+Kz)\vec j \end{array}\)
2. L'onde résultant de la superposition de ces ondes progressive et régressive est :
\(\vec E=\vec{E_p}+\vec{E_r}=E_0[\cos(\omega t-Kz)+\cos(\omega t+Kz)]\vec i=2E_0\cos\omega t.\cos Kz.\vec i\)
\(\vec B=\vec{B_p}+\vec{B_r}=\frac{E_0}{c}[\cos(\omega t-Kz)-\cos(\omega t+Kz)]\vec j=2\frac{E_0}{c}\sin\omega t. \sin Kz.\vec j\)
Cette onde est stationnaire. Les nœuds de vibration de \(\vec E\) (pour \(\cos Kz = 0\)) sont déphasés de \(p/2\) par rapport aux nœuds de vibration de \(\vec B\) (pour \(\sin Kz = 0\)).
3. Ce n'est que dans le cas où l'on a une onde plane qui se propage que les champs \(\vec E\) et \(\vec B\) sont reliés par la relation : \(\vec B=\frac{1}{c}\vec u\land\vec E\).
Cette relation intervient pour démontrer que l'énergie de la partie "électrique" est égale à l'énergie de la partie "magnétique". Mais dans tous les cas, la densité d'énergie d'une onde électromagnétique est la somme d'une partie "électrique" et d'une partie "magnétique" :
\(w=\frac{\varepsilon E^2}{2}+\frac{B^2}{2\mu}\)
Dans le cas d'une onde stationnaire, on définit encore le vecteur de Poynting par la relation \(\vec S=\frac{1}{\mu}\vec E\land\vec B\) qui représente le flux d'énergie de cette onde.
En reportant : \(\vec E=\vec{E_p}+\vec{E_r}, \vec B=\vec{B_p}+\vec{B_r}\) et en développant le produit vectoriel, on trouve \(\vec S=\frac{1}{\mu}(\vec{E_p}+\vec{E_r})\land(\vec{B_p}+\vec{B_r})=\frac{1}{\mu}(\vec{E_p}\land\vec{E_p})+ \frac{1}{\mu}(\vec{E_r}\land\vec{E_r})+\frac{1}{\mu}(\vec{E_r}\land\vec{B_p}+\vec{E_p}+\vec{B_r})\)
soit : \(\vec S=\vec{S_p}+\vec{S_r}+\frac{1}{\mu}(\vec{E_r}\land\vec{B_p}+\vec{E_p}\land\vec{B_r})\)
En un point quelconque de l'espace, le vecteur de Poynting de la somme de l'onde progressive et de l'onde régressive ne se réduit donc pas à la somme des vecteurs de Poynting de l'onde progressive et de l'onde régressive : il y a 2 termes en plus...
En résumé :
l'énergie totale d'une onde stationnaire est toujours la somme d'une partie "électrique" et d'une partie "magnétique".
mais l'énergie totale d'une onde stationnaire n'est pas toujours la somme de l'énergie totale de l'onde progressive et de l'énergie totale de l'onde régressive (qui, par exemple, prend naissance par réflexion de l'onde progressive) : seules s'ajoutent toujours les amplitudes des champs électriques respectivement magnétiques des ondes progressive et régressive.
Pour l'onde stationnaire : \(E=E_x=2E_0\cos\omega t.\cos Kz \textrm{ et } B=B_y=\frac{2E_0}{c}\sin\omega t.\sin Kz\)
\(\Rightarrow\) Densité totale d'énergie :
\(w=\frac{\varepsilon E^2}{2}+\frac{B^2}{2\mu}=\frac{\varepsilon}{2}4E_0^2\cos^2\omega t.\cos^2Kz+\frac{ 4E_0^2}{2\mu c^2}\sin^2\omega t.\sin^2Kz\)
\((2\mu c^2=1)\Rightarrow \omega=2.\varepsilon.E_0^2\cos^2\omega t.\cos^2Kz+2.\varepsilon.E^2_0\sin^2\omega t.\sin^2Kz\)
Densité totale d'énergie :
\(w\)=densité d'énergie électrique+ densité d'énergie magnétique
4.
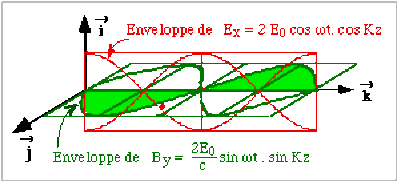
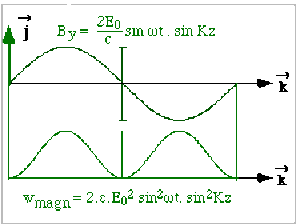
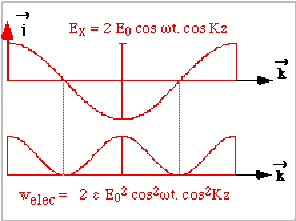
Les schémas ci-dessus représentent les champs et les densités d'énergie en fonction de \(z\), à \(t\) fixé. On pourrait faire les mêmes schémas en fonction du temps \(t\), à \(z\) fixé.
\(w_{\textrm{\'elec}}=2.\varepsilon.E_0^2\cos^2\omega t.\cos^2Kz\)
\(=\frac{\varepsilon E_0^2}{2}(\cos2\omega t+1).(\cos2Kz+1)\)
\(w_{magn}=2.\varepsilon.E_0^2\sin^2\omega t.\sin^2Kz\)
\(=\frac{\varepsilon E_0^2}{2}(1-\cos2\omega t).(1-\cos2Kz)\)
ont pour périodes :
temporelle : \(\frac{T}{2}\)
spatiale : \(\frac{\lambda}{2}\)
Ces densités d'énergie sont déphasés de \(\frac{\pi}{2}\) : quand l'une s'annule, l'autre est maximum. La densité d'énergie totale oscille entre sa partie électrique \(w_{\textrm{\'elec}}\) et sa partie magnétique \(w_{magn}\).
5. Vecteur de Poynting
\(\vec E=E_x\vec i \textrm{ et }\vec B=B_y\vec j\Rightarrow\) \(\vec S=\frac{1}{\mu}\vec E\land\vec B=\frac{1}{\mu}\vec kE_x.B_y\)
\(\Rightarrow S_z=\frac{4E_0^{2}}{\mu c}\sin\omega t.\cos\omega t.\sin Kz.\cos Kz=\frac{E_0^2}{\mu c}\sin2\omega t.\sin2Kz\).
\(\Rightarrow\) Dans une onde stationnaire, le vecteur de Poynting est lui-même stationnaire :
sa période temporelle et sa période spatiale sont la moitié de la période temporelle \(T\) et de la longueur d'onde \(\lambda\) de l'onde électromagnétique,
il oscille au cours du temps, de sorte que sa valeur moyenne est nulle sur une demi-période \(\frac{T}{2}\) du champ électromagnétique,
il oscille en fonction de la variable \(z\) (qui définit la stationnarité), de sorte que sa valeur moyenne est nulle sur une demi-longueur d'onde \(\frac{\lambda}{2}\) du champ électromagnétique.