Oscillations libres non amorties

Cette étude concerne les oscillations libres de systèmes non-amortis, ayant \(N\) de degrés de liberté (revoir la définition donnée en Introduction).

La question que l'on se pose est celle de l'expression de la vibration générale, puis celle de la détermination de la vibration particulière prise par ce système consécutivement à des conditions initiales de lancement.

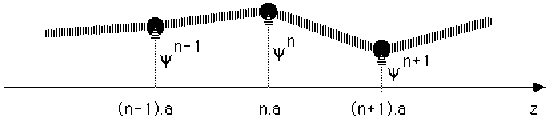
Dans ce chapitre, on considère une "corde plombée" par \(N\) masses, i.e. une chaîne de \(N\) masses ponctuelles, séparant \(N+1\) ressorts identiques considérés eux-mêmes sans masse. Les extrémités de cette chaîne sont situés en \(z = 0\) et \(z = L\) et sont fixes, ce qui constitue "les conditions aux limites" du système.

Pour traiter la vibration la plus générale de ce système, il faut considérer que chaque masse a \(3\) degrés de liberté (\(1\) degré pour décrire le mouvement le long de l'axe \(z\), et \(2\) degrés pour décrire le mouvement transversal). Pour traiter uniquement la vibration transversale, chaque masse possède alors \(2\) degrés de liberté.

Par exemple, le système constitué de \(2\) masses et \(3\) ressorts possède \(4\) degrés de liberté pour ce qui concerne ses vibrations transversales.

On déterminera en exercice :

- la vibration générale de ce système, puis

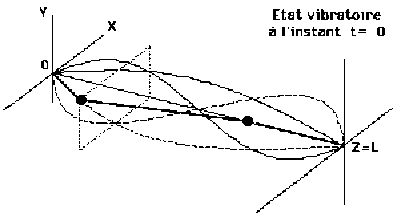
- sa vibration particulière consécutive aux conditions initiales représentées ci-contre.

Dans ce qui suit, on impose un "guidage" sans frottement au mouvement des masses (voir le schéma suivant) :

• la vibration est donc transversale dans une seule direction notée \(O_y\).

• ce système de \(N\) masses a donc \(N\) degrés de liberté.

• l'état du système est représenté par un vecteur noté \(Y\), dans un espace de dimension \(N\), où la composante de rang \(n\) notée \(Y^n\) représente l'amplitude de vibration de la n-ième masse.

Dans ce chapitre, on considère le cas : \(N\) fini.

On déterminera, au chapitre suivant, ce que devient l'expression générale des oscillations du système lorsqu'on effectue le passage à la limite : \(N\) tendant vers l'infini.

On accepte toutes les limitations nécessaires pour pouvoir considérer ce système comme linéaire : dans ces conditions, le couplage exercé entre masses voisines par chaque ressort est une force proportionnelle à son allongement, et on ne considère que les "petites oscillations" (la droite passant par 2 masses consécutives quelconques s'écarte peu de la direction \(Oz\) du système à l'équilibre).

Quant au choix de ce type de système, on peut noter que :

• Un ressort joint toujours les \(2\) masses les plus proches : il s'agit là d'un système où le couplage intervient par l'interaction entre les seuls plus proches voisins. Cette interaction très particulière est cependant représentative d'une large classe de phénomènes.

• Les résultats concernant les vibrations transversales de ce système mécanique peuvent s'étendre par analogie au cas des vibrations (transversales) d'un champ électromagnétique.

Avec la modélisation annoncée, on va montrer que :

• les équations se mettent sous la forme matricielle : \(\ddot \Psi = U . \Psi\)

• la matrice \(U\) n'est pas diagonale, mais elle ne comporte de termes non nuls que sur la diagonale et sur les rangées situées respectivement au-dessus et au-dessous de la diagonale.

• une telle matrice "presque diagonale" est d'un type mathématique que l'on sait diagonaliser. (La démonstration permettant de trouver les coefficients de la matrice de changement de base \(M\) est reportée en annexe).