Oscillations libres non amorties

On applique ici la technique générale consistant à rechercher la matrice \(M\) de changement de base,

• telle que \(\Psi = M.\phi\)

• et que sur la nouvelle base (en coordonnées \(\phi\)) la matrice du système soit diagonale.

Notons \(U_d\) cette matrice diagonale.

Dans ces conditions, l'équation précédente \(\ddot \Psi = U . \Psi\) est remplacée par la nouvelle équation :

\(\begin{array}{l} \ddot \phi = U_d . \phi \\ \ddot \Psi = M . \ddot \phi = M . U_d . \phi \end{array} \Rightarrow ~~ M . U_d = U . M\)

On pose : \(~~ U_d = \left| \begin{array}{cccccccc} -\omega_1^2 & . & 0 & . \\ . & -\omega_2^2 & . & . \\ 0 & . & -\omega_n^2 & . \\ . & . & . & -\omega_N^2 \end{array} \right|\)

de sorte que la composante de rang \(p\) de la relation \(\ddot \phi = U_d . \phi\) s'écrit : \(\ddot \phi^p = - \omega_p^2 . \phi^p\)

et admet une solution générale de pulsation \(\omega_p\) , soit :

\(\phi^p = A^p . \cos (\omega_p.t + a_p)\)

La matrice de changement de base \(M\) peut s'exprimer comme ligne de vecteurs \(M_p\) , soit :

\(M = \left| \begin{array}{cccccccc} M_1^1 & M_2^1 & M_3^1 & \mathrm{ }.\mathrm{ } & \mathrm{ }.\mathrm{ } & M_N^1 \\ M_1^2 & M_2^2 & M_3^2 & . & . & M_N^2 \\ M_1^3 & M_2^3 & M_3^3 & . & . & M_N^3 \\ . & . & . & . & . & . \\ M_1^N & M_2^N & M_3^N & . & . & M_N^N \end{array} \right| = |M_1 , M_2 , ..., M_p , ..., M_N|\)

D'où :

\(M . U_d = |M_1 , M_2 , ..., M_p , ..., M_N| . \left| \begin{array}{cccccccc} -\omega_1^2 & 0 & . & 0 \\ 0 & -\omega_2^2 & . & 0 \\ 0 & . & . & 0 \\ 0 & . & . & -\omega_N^2 \end{array} \right|\)

soit : \(M . U_d = |- \omega_1^2 . M_1 , - \omega_2^2 . M_2 , ... , - \omega_p^2 . M_p , - \omega_N^2 . M_N|\)

On calcule de même :

\(U . M = U . |M_1, M_2, ..., M_p, ..., M_N| = |U . M_1, U . M_2, ..., U . M_p, ..., U . M_N|\) .

Soit en identifiant :

Les \(M_p\) sont vecteurs propres de la matrice \(U\), aux valeurs propres \(-\omega_p^2\) .

Les \(\omega_p^2\) satisfont donc l'équation générale aux pulsations propres \(\textrm{d\'et} ( U + \omega^2.I ) = 0\) ,

où \(I\) désigne la matrice unité de dimension \(N\) .

Les solutions \(\omega_p\) permettent alors d'expliciter les modes propres \(\phi_p\) en coordonnées \(\phi\)

\(\phi_p = \left| \begin{array}{c} 0 \\ . \\ \phi^p \\ . \\ 0 \end{array} \right| \)avec \(\phi^p = A^p . \cos (\omega_p . t + \alpha_p)\)

La connaissance des \(M_p\) permet d'en déduire l'expression générale de la vibration en coordonnées \(\Psi\) par la relation : \(\Psi = M.\phi\) , soit :

\(\Psi = \left| \begin{array}{c} \Psi^1 \\ \Psi^2 \\ . \\ . \\ \Psi^N \end{array} \right| = |M_1, M_2, ..., M_N| . \left| \begin{array}{c} \phi^1 \\ \phi^2 \\ . \\ . \\ \phi^N \end{array} \right| = M_1 . \phi^1 + M_2 . \phi^2 + ... + M_N . \phi^N\)

soit : \(\Psi = \Psi_1 + \Psi_2 + ... + \Psi_N\)

Dans le mode propre de rang \(p\), la vibration de l'ensemble des \(N\) variables décrivant le système est donc définie par :

\(\Psi_p = M_p . \phi^p = \left| \begin{array}{c} M_p^1 \\ M_p^2 \\ M_p^3 \\ ... \\ M_p^N \end{array} \right| . A^p . \cos (\omega_p . t + \alpha_p)\)

Dans le mode propre de rang \(p\), le mouvement du n-ième plomb est décrit par l'expression de la n-ième coordonnée soit : \(\Psi_p^n = M_p^n . A^p . \cos (\omega_p . t + \alpha_p)\)

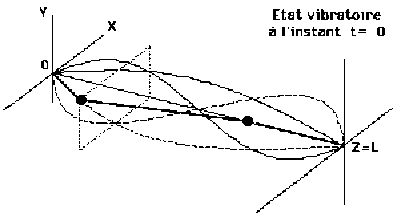
Reprenons l'exemple du système constitué de \(3\) ressorts et de \(2\) masses assujetties à des vibrations transversales, tel que les extrémités de ce système sont fixes (en \(z=0\) et \(z=L\)).

La vibration générale de ce système s'exprime sur la base des \(4\) modes propres :