Définition
Définition : Définition d'une matrice
Soit deux entiers \(n\) et \(p\) supérieurs ou égaux à \(1\). On appelle matrice de type(n,p) à coefficients dans \(\mathbf K\), un tableau rectangulaire à \(n\) lignes et \(p\) colonnes d'éléments de \(\mathbf K\).
On dit aussi que \(\mathcal A\) est une matrice \(n\times p\) . Un tel tableau est représenté de la façon suivante :
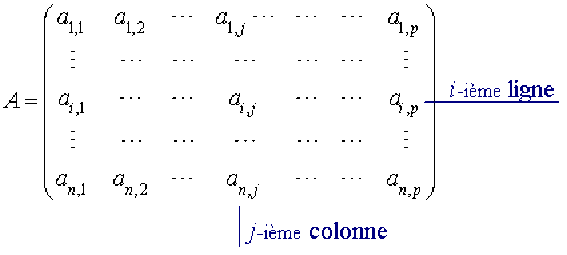
Remarque :
En fait, si on désigne par \(\mathcal I\) l'ensemble des entiers compris entre \(1\) et \(n\) et par \(\mathcal J\) l'ensemble des entiers compris entre \(1\) et \(p\), se donner une matrice revient à se donner une application de \(\mathcal I\times\mathcal J\) dans \(\mathcal K\), le coefficient \(a_{i,j}\) représentant l'image du couple \((i,j)\) par cette application.