Matrices à n lignes et p colonnes

Les éléments \(a_{i,j}\) de \(\mathcal K\) sont appelés les coefficients de la matrice \(\mathcal A\). Le premier indice est l'indice de la ligne, le deuxième celui de la colonne, donc \(a_{i,j}\) désigne l'élément de la i-ième ligne et j-ième colonne.

On notera souvent une telle matrice \(\displaystyle{\mathcal A=(a_{i,j})_{\begin{array}{cccccc}1\leq i\leq n\\1\leq j\leq p\end{array}}}\) ou encore \(\mathcal A=(a_{i,j})\), s'il n'y a pas d'ambiguïté, et l'on dira aussi que \(a_{i,j}\) est le terme général de la matrice.

Autrement dit on a le schéma :

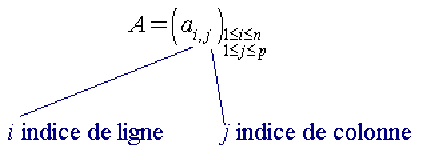
On trouve aussi dans la littérature mathématique la notation\( [a_{i,j}]\), mais nous utiliserons la première notation indiquée. L'ensemble des matrices à \(n\) lignes et \(p\) colonnes à coefficients dans \(\mathcal K\) est noté \(\mathcal M_{n,p}(\mathbf K)\).