Biprisme de Fresnel (2)
Durée : 5 mn
Note maximale : 2
Question
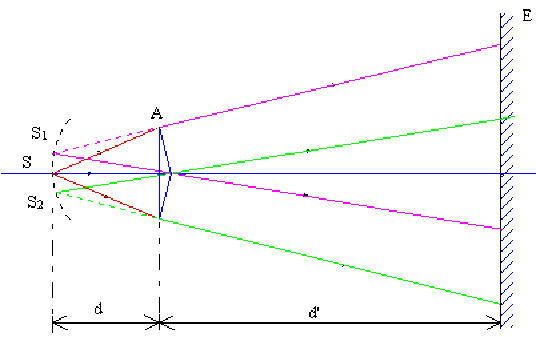
Un biprisme de Fresnel d'angle \(A = 0,006~\textrm{rad}\) , d'indice \(n = 1,5\) est éclairé par une fente fine perpendiculaire au plan de section principale et située à une distance \(d = 20~\textrm{cm}\) du biprisme. On observe des franges sur un écran situé à une distance \(d' = 1 \textrm m\) du biprisme en utilisant un faisceau de lumière monochromatique de largeur d'onde dans le vide \(\lambda = 5000~ Å\).
b) calculer le nombre de franges sombres sur l'écran
Solution
Sur l'écran, la demi-largeur \(l\) du champ d'interférences est : \(l=d.\tan D~\#~d(n-1).A=\textrm{1,5 mm}\)
le nombre de franges sombres s'obtient en comptant le nombre d'interfranges contenu dans \(l\) : \(n = l / i = 3\)
On a donc bien \(3\) franges noires de chaque côté de la frange centrale soit au total \(2\times3=6\) franges noires.
[1 pt]
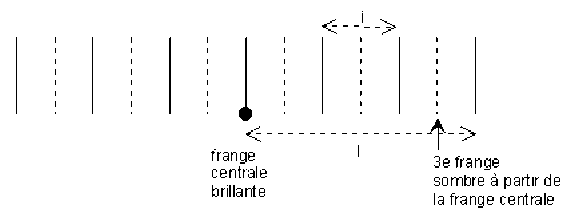
En divisant la largeur totale \(2l\) du champ d'interférence par \(i\), on pourrait compter une frange noire en trop. Les franges noires sont repérées par
\(x = ( 2 k + 1 )/2 . i\) avec \(k = \pm 1 , \pm 2 ...\)
[1 pt]