Stigmatisme approché [Dioptre Sphérique]

Stigmatisme approché

Image d'un point sur l'axe :

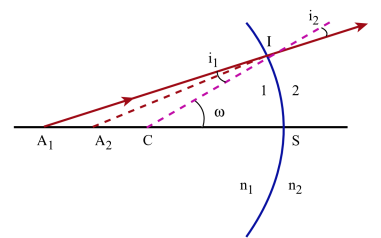
Pour qu'il y ait stigmatisme^[1] approché, il faut que la position de \(A_{\mathit2}\) sur l'axe du dioptre ne dépende pratiquement pas de \(\omega\).

Si l'on reprend la relation :

\(\frac{\overline{\mathrm{IA}_2^2}}{\overline{\mathrm{IA}_1^2}}=\frac{\mathrm n_2^2~\overline{\mathrm{CA}_2^2}}{\mathrm n_1^2~\overline{\mathrm{CA}_1^2}}=\frac{\overline{\mathrm{CA}_2^2}+\overline{\mathrm{CS}^2}-2.\overline{\mathrm{CA}_2}.\overline{\mathrm{CS}}.\cos\omega}{\overline{\mathrm{CA}_1^2}+\overline{\mathrm{CS}^2}-2.\overline{\mathrm{CA}_1}.\overline{\mathrm{CS}}.\cos\omega}\)

cette condition est vérifiée dans les cas suivants :

le coefficient de \(\cos~\omega\) est très petit: ce qui correspond aux points voisins du centre, du sommet ou voisins des points de Weïerstrass (confirmant ainsi que, par raison de continuité, les points présentant un stigmatisme approché doivent être recherchés au voisinage des points présentant un stigmatisme rigoureux).
\(\cos~\omega\) est constant c'est à dire que \(\omega\) est voisin de zéro : on est alors dans l'approximation de Gauss^[2] :

dans ce cas le point I est voisin du sommet du dioptre S et on peut écrire la relation :

\(\mathrm n_1~\frac{\overline{\mathrm{CA}_1}}{\overline{\mathrm{IA}_1}}=\mathrm n_2~\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{IA}_2}}\) sous la forme : \(\mathrm n_1~\frac{\overline{\mathrm{CA}_1}}{\overline{\mathrm{SA}_1}}=\mathrm n_2~\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{SA}_2}}\)

On pourra alors énoncer :

« il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux^[3]. »

Simuler

L'animation suivante illustre les propriétés de stigmatisme du dioptre sphérique :

Stigmatisme approché

Notes

Stigmatisme
Propriété d'un système optique qui associe un seul point image à un seul point source. Un système peut n'être stigmatique que pour certains points remarquables. Pour un système stigmatique, tous les rayons issus d'un point source du domaine de stigmatisme, convergent vers le (ou proviennent du) même point image. Le stigmatisme est dit rigoureux lorsque le chemin optique entre le point objet et le point image est indépendant du rayon. Le stigmatisme est dit approché lorsque les conditions de Gauss sont nécessaires pour qu'il soit réalisé.
Exemple de système non stigmatique pour le couple de points \(AA'\) : le rayon \(APP"A"\) ne passe pas par \(A'\), image de \(A\) par d'autres rayons.
Un dioptre plan n'est pas stigmatique.
Conditions de GAUSS
Un système est utilisé dans les conditions de Gauss, lorsque les rayons qui le traversent sont peu inclinés sur l'axe principal ( rayons paraxiaux).
On peut alors considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (a~sina).
Dans ces conditions, il y a stigmatisme pour les points objet et image.
Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.
C'est en 1841 que Gauss a, le premier, présenté un exposé sur la formation des images dans cette approximation. Depuis, on emploie également les termes d'approximation de Gauss ou d'optique Gaussienne.
Rayons Paraxiaux
Les rayons peu inclinés sur l'axe principal sont appelés rayons paraxiaux.
Lorsqu'on se limite à l'étude de tel rayons, on peut considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (\(a~\approx~\sin~a\)).
On dit alors qu'on travaille dans les conditions de GAUSS.
Dans ces conditions, il y a stigmatisme pour les points objet et image. Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.