Physique
Dioptre Sphérique
Précédent
Suivant
- Dioptre Sphérique
- Apprendre
- Définitions
- Stigmatisme rigoureux...
- Stigmatisme approché
- Image du centre
- Foyer image
- Foyer objet
- Plan focal image
- Plan focal objet
- Image d'un objet plan...
- Construction du rayon r...
- Origine au centre
- Origine au sommet
- Origines aux foyers
- Relation de Lagrange He...
- Dioptre convergent
- Dioptre divergent
- Ce qu'il faut retenir :...
- Simuler
- Observer
- S'exercer
- S'évaluer
- Apprendre
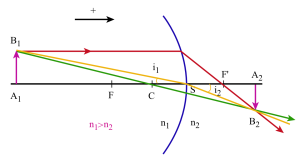
| Origine au sommet |
Formules de conjugaison
En reprenant la relation :
on peut l'écrire sous la forme :
Si l'on considère les triangles SA1B1 et SA2B2 on a :
et
on en déduit alors :
Comme nous nous situons dans l'approximation de Gauss , nous avons :
et
d'autre part :
d'où :
