Foyer image
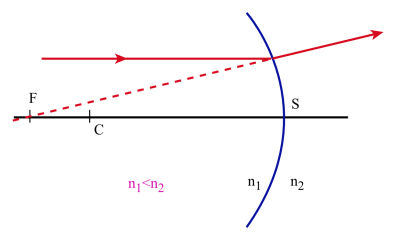
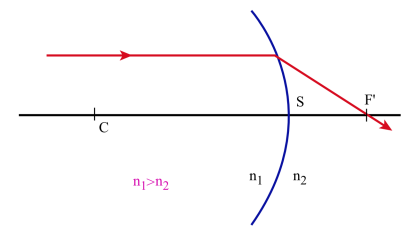
Lorsque le point A1 est très loin sur l'axe on peut confondre CA1 et SA1 et la relation :
\(\mathrm n_1~\frac{\overline{\mathrm{CA}_1}}{\overline{\mathrm{SA}_1}}=\mathrm n_2~\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{SA}_2}}~~\) peut s'écrire en appelant F' le foyer image[2] du dioptre :
\(\frac{\overline{\mathrm{SF'}}}{\overline{\mathrm{CF'}}}=\frac{\mathrm n_2}{\mathrm n_1}\)
on en déduit la relation donnant la position du foyer F' par rapport au sommet S :
\(\overline{\mathrm{SF'}}=\overline{\mathrm{CS}}~\frac{\mathrm n_2}{\mathrm n_1~-~\mathrm n_2}\)
Cette quantité notée f' est appelée distance focale image du dioptre sphérique.
Dans le cas du dioptre concave : \(\overline{\mathrm{CS}}>0\)
si n1 < n2, F' est virtuel
si n1 > n2, F' est réel
Il résulte de cette définition que tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image[2] F'.
Observer
Le foyer image d'un dioptre sphérique est visualisé dans la vidéo suivante :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.