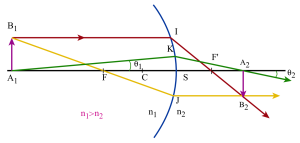
Relation de Lagrange Helmholtz [Dioptre Sphérique]

Relation de Lagrange Helmholtz

Si A₂B₂ est l'image^[1] de A₁B₁ un rayon issu de A₁ se réfracte en K en passant par A₂. Si l'on choisit le sens trigonométrique comme sens positif des angles on peut écrire :

\(\overline{\mathrm{SK}}=-\overline{\mathrm{SA}_1}~\tan~\theta_1=-\overline{\mathrm{SA}_2}~\tan~\theta_2\)

puisque nous nous plaçons dans l'approximation de Gauss^[2] on pourra confondre les tangentes des angles avec les angles exprimés en radians :

\(\overline{\mathrm{SA}_1}~\theta_1=\overline{\mathrm{SA}_2}~\theta_2\)

nous avons vu que :

\(\gamma=\frac{\mathrm n_1}{\mathrm n_2}~\frac{\overline{\mathrm{SA}_2}}{\overline{\mathrm{SA}_1}}=\frac{\overline{\mathrm A_2\mathrm B_2}}{\overline{\mathrm A_1\mathrm B_1}}\)

soit encore : \(\mathrm n_1~.~\overline{\mathrm A_1\mathrm B_1}~.~\overline{\mathrm{SA}_2}=\mathrm n_2~.~\overline{\mathrm A_2\mathrm B_2}~.~\overline{\mathrm{SA}_1}\)

on en déduit facilement le relation de Lagrange-Helmholtz :

\(\mathrm n_1~.~\overline{\mathrm A_1\mathrm B_1}~.~\theta_1=\mathrm n_2~.~\overline{\mathrm A_2\mathrm B_2}~.~\theta_2\)

Notes

Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Conditions de GAUSS
Un système est utilisé dans les conditions de Gauss, lorsque les rayons qui le traversent sont peu inclinés sur l'axe principal ( rayons paraxiaux).
On peut alors considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (a~sina).
Dans ces conditions, il y a stigmatisme pour les points objet et image.
Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.
C'est en 1841 que Gauss a, le premier, présenté un exposé sur la formation des images dans cette approximation. Depuis, on emploie également les termes d'approximation de Gauss ou d'optique Gaussienne.