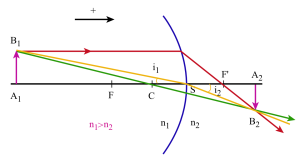
Origine au centre
Formules de conjugaison
En reprenant la relation : \(\mathrm n_1~\frac{\overline{\mathrm{CA}_1}}{\overline{\mathrm{SA}_1}}=\mathrm n_2~\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{SA}_2}}~~\)
on peut encore écrire : \(\mathrm n_1~\frac{\overline{\mathrm{SA}_2}}{\overline{\mathrm{CA}_2}}=\mathrm n_2~\frac{\overline{\mathrm{SA}_1}}{\overline{\mathrm{CA}_1}}~~\)
sachant que :
\(\overline{\mathrm{SA}_1}=\overline{\mathrm{SC}}~+~\overline{\mathrm{CA}_1}\)
\(\overline{\mathrm{SA}_2}=\overline{\mathrm{SC}}~+~\overline{\mathrm{CA}_2}\)
on en déduit :
\(\frac{\mathrm n_1}{\overline{\mathrm{CA}_2}}-\frac{\mathrm n_2}{\overline{\mathrm{CA}_1}}=\frac{\mathrm n_1~-~\mathrm n_2}{\overline{\mathrm{CS}}}\)
En appliquant le théorème de Thalès aux triangles CA1B1 et CA2B2 on obtient : \(\gamma=\frac{\overline{\mathrm{A}_2\mathrm{B}_2}}{\overline{\mathrm{A}_1\mathrm{B}_1}}=\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{CA}_1}}\)