Définitions
Définition : Fonction
On appelle fonction \(f\) d'un ensemble \(E\) vers un ensemble \(F,\) une application qui à tout élément \(x\in E\) fait correspondre un unique élément \(y\in F.\)
Notation : \(\color{red} f : x\mapsto f (x)\) ou \(\color{red} y = f (x)\)
Définition : Fonction scalaire
La fonction est dite fonction scalaire, ou fonction numérique si les ensembles de départ \(E\) et d'arrivée \(F\) sont de sous-ensembles de \(R.\)
Exemple :
\(\begin{array}{l l}f_1 : x\mapsto y_1 = x^2 &E = F = R\\ f_2 : x\mapsto y_2 = \cos x & E = R~\textrm{et}~F = [ -1 , +1 ] \\ f_3 : x\mapsto y_3 = \arcsin x & E = [ -1 , +1 ]~\textrm{et}~F = [ - \pi/2 , \pi /2 ]\end{array}\)
Définition : Domaine de définition
On appelle ensemble de définition \(\color{red} (D_f ),\) l'ensemble des nombres réels qui ont une image \(f (x)\) dans \(R.\)
Exemple :
\(\begin{array}{l l}f :x\mapsto y = \frac{1}{x^2}&D_f=R^*\\g :x\mapsto y = \sqrt{\frac{x}{1-x}}&D_g=[0,1[\end{array}\)
Définition : Graphe
La courbe \((C)\) représentative des points \(f (x)\) quand la variable \(x\) décrit le domaine de définition est appelé graphe de \(f\) dans \(R.\)
Exemple :
Fonction affine : \(y_1 = x+1\)
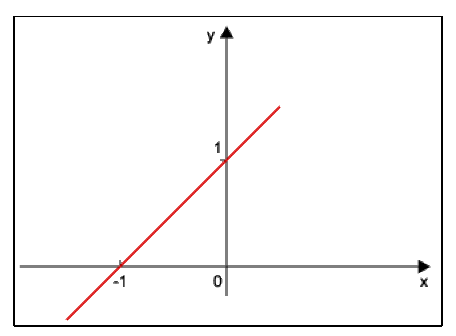
Fonction puissance : \(y_2 = x^2\)
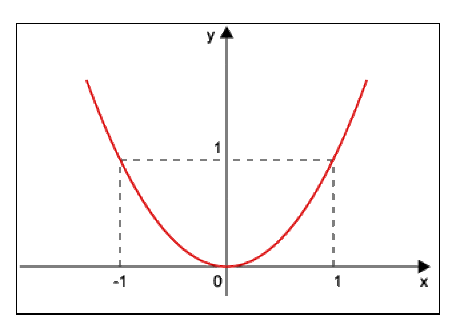
Fonction trigonomètrique : \(y_3 = \cos x\)
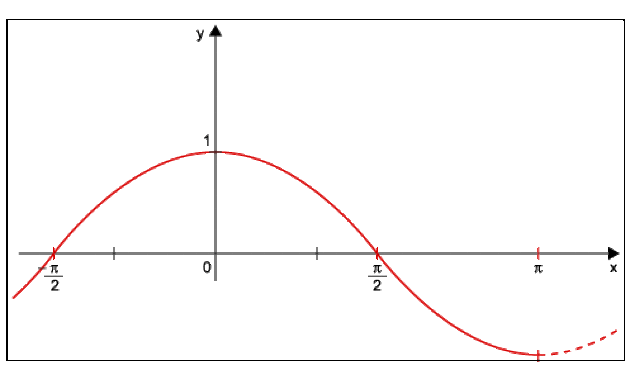
Fonction hyperbolique : \(y_4 = \textrm{sh} x\)
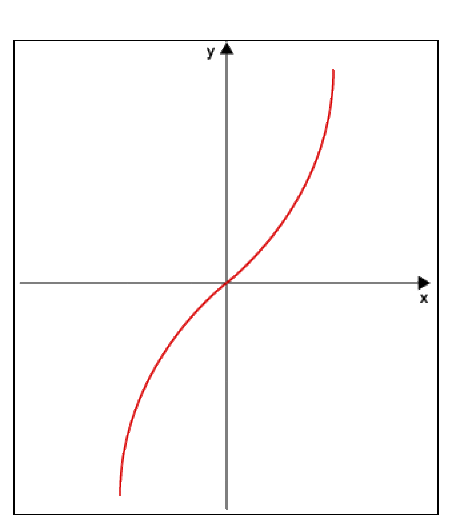
Définition : Fonction réciproque
On appelle fonction réciproque \(\color{red}f^{-1},\) si elle existe, l'application de \(F\) dans \(E\) qui à chaque élément \(y\in F\) fait correspondre un élément unique \(x\in E.\)
Notation : \(\color{red}f^{- 1} : y\mapsto x = f^{-1} (y)\)
\(\color{red}F\mapsto E\)
Les graphes \((C)\) de \(f (x)\) et \((C^{-1})\) de \(f^{-1}(x)\) sont symétriques par rapport à la droite d'équation \(y = x.\)
Exemple :
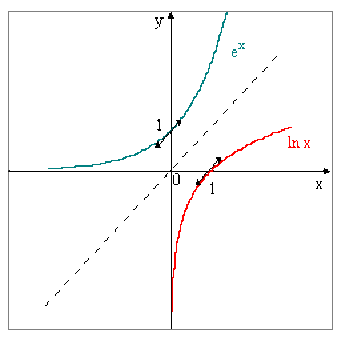
Les fonctions réciproques sont symétriques par rapport à la droite \(y = x.\)
Cas de \(e^x\) et \(\ln x\)
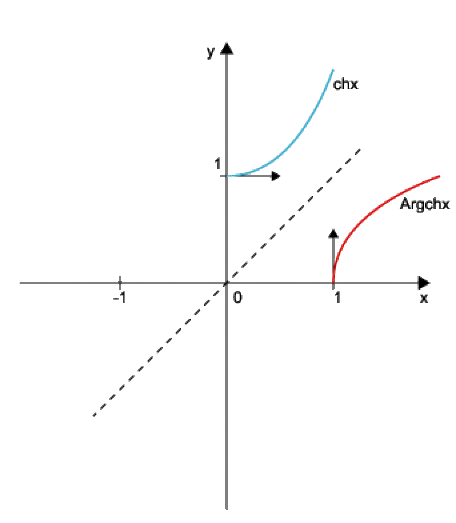
Cas de \(\textrm{ch} x\) et \(\textrm{Argch} x\)
Définition : Fonction composée d'une variable
On appelle fonction composée de \(x,\) une fonction \(f (u)\) où la variable \(u\) est elle-même fonction d'une autre variable \(x.\)
Notation : \(\color{red}f (u) = f [ u(x) ] = (f \circ u)(x)\)
Exemple :
Fonctions :
\(y_1 = \sin(3x+1)\) est la composée de \(y_1 = \sin u\) avec \(u = 3x+1\)
\(y_2 = e^{x^2}\) est la composée de \(y_2 = e^v\) avec \(v = x^2\)
\(y_3 = (x^3+2)^4\) est la composée de \(y_3 = w^4\) avec \(w = x^3+2\)