Interprétation géométrique de la dérivée et de la différentielle
Soient les points : \(M ( x, f (x) )\) et \(M' (x + \Delta x, f (x + \Delta x))\) appartenant au graphe \((C)\) de \(f\) et la tangente \(MT\) à la courbe au point \(M.\)
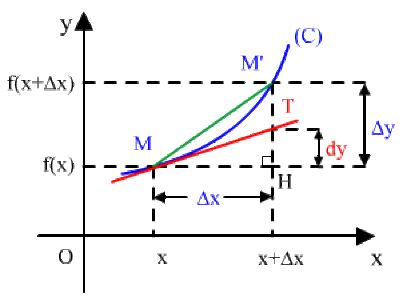
A l'accroissement \(\Delta x\) de la variable correspond l'accroissement \(\Delta y\) de la fonction représentée par \(\overline{HM'}.\)
La pente de la corde \(MM'\) est définie par \(\frac{\Delta y}{\Delta x}=\frac{\overline{HM'}}{\overline{MH}}\)
La dérivée de \(f~\textrm{au point}~M~\textrm{sera}~\)
\(f'(x)=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\color{red}\begin{array}{c}\textrm{pente de la tangente } MT\\ \textrm{au point }M\textrm{ à la courbe }(C)\end{array}\)
La différentielle de \(f\) : \(df=f'(x)\Delta x=\overline{HT}\)
On remarquera que \(\Delta f \rightarrow df\) quand \(\Delta x \rightarrow 0\)