Circuit RLC - Régime transitoire
Partie
Question
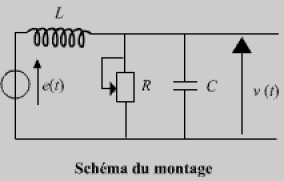
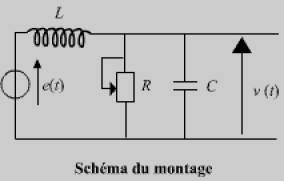
Soit le circuit RLC, alimenté par une tension échelon \(e(t)\).
L'étude portera sur la détermination de \(v(t)\) aux bornes du condensateur \(C\).
Caractéristiques du circuit :
Bobine de \(250 \textrm{trs}\) : \(L \approx 2,2 \textrm{mH}, r = 0,6 \textrm{W}\)
Condensateur : \(C \approx 0,23 µ\textrm{F}\)
La tension échelon \(e(t)\) est définie par : \(t < 0\), \(e(t) = 0\) et pour \(t \geq 0\), \(e(t) = E_{0}~~\textrm{constant}\)
Montrer que \(v(t)\) vérifie l'équation différentielle : \(\frac{\textrm{d}^{2}\nu}{\textrm{d}t^{2}} + \frac{1}{\tau} \frac{\textrm{d}\nu}{\textrm{d}t} = \omega_{0}^{2}~\nu = \omega_{0}^{2} e(t)\).
On posera : \(\tau = RC\) (constante de temps)
\(\omega_{0}^{2} = 1 / LC\)
Aide simple
Déterminer par exemple, le courant \(i(t)\) dans le circuit source et écrire la loi d'ohm dans une maille contenant la bobine \(L\).
Aide détaillée
Remplaçons \(i(t)\) dans l'équation de maille :
\(e(t) = L \frac{\textrm{d}i}{\textrm{d}t} + \nu(t)\)
afin d'obtenir l'équation différentielle proposée.
Solution simple
La courant \(i(t)\) a pour expression \(i(t) = \frac{1}{R}~\left( \nu (t) + RC~\frac{\textrm{d} \nu}{\textrm{d} t}\right)\)
sachant que \(e(t) = L~\frac{\textrm{d}i}{\textrm{d}t}+\nu (t)\), la substitution de \(i(t)\) dans cette équation conduit à l'équation différentielle :
\(LC \frac{\textrm{d}^{2} \nu}{\textrm{d}t^{2}} + \frac{L}{R} \frac{\textrm{d} \nu}{\textrm{d} t} + \nu = e(t)\)
Solution détaillée
Posons \(i(t)\) courant dans le circuit source \(e(t)\) et \(i'(t)\) celui dans la branche contenant le condensateur.
Aux bornes de la résistance \(\nu (t) = R (i - i')\), or, pendant la charge du condensateur, le courant vérifie la relation :
\(i'(t) = \frac{\textrm{d}q(t)}{\textrm{d}t} = C \frac{\textrm{d} \nu}{\textrm{d} t}\)
d'où \(\nu(t) = R~\left( i - C~\frac{\textrm{d} \nu}{\textrm{d} t} \right) \Rightarrow i(t) = \frac{1}{R}~\left( \nu(t) + RC \frac{\textrm{d} \nu}{\textrm{d}t} \right)\)
Puisque \(e(t) = L~\frac{\textrm{d}i}{\textrm{d}t} + \nu(t) = \frac{L}{R} \left( \frac{\textrm{d}\nu}{\textrm{d}t} + RC \frac{\textrm{d}^{2} \nu}{\textrm{d}t^{2}} \right) + \nu(t)\),
c'est à dire \(\textcolor{red}{LC \frac{\textrm{d}^{2} \nu}{\textrm{d} t^{2}} + \frac{L}{R} \frac{\textrm{d}\nu}{\textrm{d}t} + \nu = e(t)}\)
Divisons tous les termes par \(LC\) et introduisons les nouvelles variables \(t\) et \(\omega_{0}^{2}\) :
\(\textcolor{red}{\frac{\textrm{d}^{2} \nu}{\textrm{d}t^{2}} + \frac{1}{\tau} \frac{\textrm{d}\nu}{\textrm{d}t} + \omega_{0}^{2} \nu = \omega_{0}^{2}~e(t)}\)
Question
Déterminer la solution générale de l'équation homogène.
Discuter les différents régimes en fonction des valeurs de \(R\) (régimes : apériodique, apériodique critique, pseudopériodique).
Aide simple
Suivant le signe du discriminant (fonction des valeurs de \(R\)), définir les différents régimes.
Aide détaillée
Posons \(\Delta\) le discriminant de l'équation caractéristique : \(r^{2} + \frac{1}{\tau} r + \omega_{0}^{2} = 0\)
Si \(\Delta > 0\) : 2 racines réelles, régime apériodique.
Si \(\Delta = 0\) : 1 racine double, régime apériodique critique.
Si \(\Delta < 0\) :
2 racines complexes conjugués, régime pseudopériodique.
2 racines imaginaires, régime oscillant sans amortissement.
Solution simple
Expression du discriminant \(\Delta\) de l'équation caractéristique :
\(\Delta = \frac{1}{\tau^{2}} - 4 \omega_{0}^{2} = \frac{R - 4 R^{2}C}{R^{2}LC^{2}}\)
1er cas :
\(\Delta > 0, \textcolor{blue}{R < \frac{1}{2} \sqrt{\frac{L}{C}}} \rightarrow\) Régime apériodique
2ème cas :
\(\Delta = 0, \textcolor{blue}{R = \frac{1}{2} \sqrt{\frac{L}{C}}} \rightarrow\) Régime apériodique critique
3ème cas :
\(\Delta < 0, \textcolor{blue}{R > \frac{1}{2} \sqrt{\frac{L}{C}}} \rightarrow\) Régime pseudopériodique
Solution détaillée
Soit l'équation différentielle homogène :
\(\frac{\textrm{d}^{2} \nu}{\textrm{d}t^{2}} + \frac{1}{\tau} \frac{\textrm{d} \nu}{\textrm{d} t} + \omega_{0}^{2} \nu = 0\),
elle admet pour équation caractéristique : \(r^{2} + \left( \frac{1}{\tau} \right) r + \omega_{0}^{2} = 0\).
Calculons le discriminant : \(\Delta = \left( \frac{1}{\tau} \right)^{2} - 4 \omega_{0}^{2} = \frac{L}{R^{2} C^{2}} - \frac{4}{LC} = \frac{L - 4R^{2}C}{R^{2}LC^{2}}\)
1er cas : \(\Delta > 0, L - 4R^{2}C > 0 \Rightarrow R < \frac{1}{2} \sqrt{\frac{L}{C}}\)
Equation caractéristique admet 2 racines :
\(r_{1} = - \frac{1}{2}~\left( \frac{1}{\tau} + \sqrt{\frac{1}{\tau^{2}} - 4 \omega_{0}^{2}} \right)\) et \(r_{2} = - \frac{1}{2}~\left( \frac{1}{\tau} - \sqrt{\frac{1}{\tau^{2}} - 4 \omega_{0}^{2}} \right)\)
La solution générale est donc : \(\textcolor{blue}{\nu(t) = K_{1} e^{r_{1} t} + K_{2} e^{r_{2}t}}\) régime périodique
2nd cas : \(\Delta = 0, L - 4 R^{2}C = 0 \Rightarrow R = \frac{1}{2} \sqrt{\frac{L}{C}}\)
Equation caractéristique admet 1 racine double :
\(r = r_{1} = r_{2} = - \frac{1}{2 \tau}\)
La solution générale est donc : \(\nu(t) = ( K_{1}t + K_{2}) e^{rt}\) régime apériodique critique
3ème cas : \(\Delta < 0, L - 4 R^{2}C < 0 \Rightarrow R > \frac{1}{2} \sqrt{\frac{L}{C}}\)
Équation caractéristique admet 2 racines complexes conjugués :
\(r = -\frac{1}{2} \left( \frac{1}{\tau} \pm j \sqrt{4 \omega_{0}^{2} - \frac{1}{\tau^{2}}}\right) = \alpha \pm j \beta\)
La solution générale est donc :
\(\nu (t) = e^{\alpha t} (K_{1} \cos{\beta t} + K_{2} \sin \beta t)\) ou \(\nu (t) = Ke^{\alpha t} \cos{(\beta t + \rho)}\) régime pseudopériodique
Application numérique :
La résistance critique \(R_{C} = \frac{1}{2} \sqrt{\frac{L}{C}} = \frac{1}{2} \sqrt{\frac{2,2.10^{-3}}{0,23.10^{-6}}} \approx \frac{10^{2}}{2} = 50 \Omega\)
Donc pour \(R < 50 \Omega\) le régime est apériodique.
pour \(R = 50 \Omega\) le régime est apériodique critique.
pour \(R > 50 \Omega\) le régime est pseudopériodique.
Pour vérifier expérimentalement :