Résonance Magnétique Nucléaire
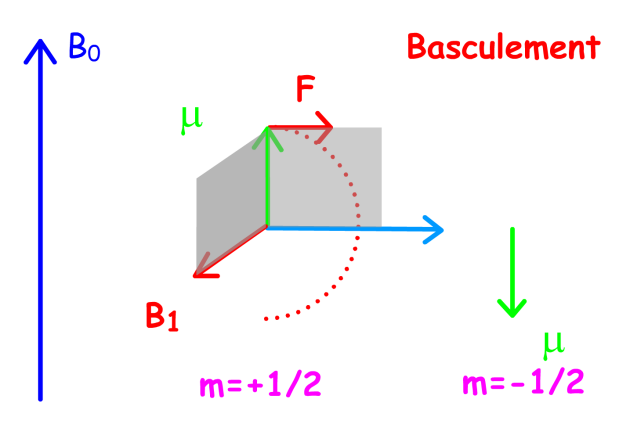
La transition de l'état magnétique \(m = +\frac{1}{2}\) vers l'état \(m = -\frac{1}{2}\) correspond à un "basculement" du vecteur moment magnétique \(\mu\). Considérons dans un premier temps les conditions de ce basculement en absence de précession.
Pour obtenir un tel basculement il est nécessaire d'appliquer un champ magnétique B1 perpendiculaire à la direction de \(\mu\) (et donc perpendiculaire à Bo) pour qu'apparaisse une force F perpendiculaire à \(\mu\) (et donc à Bo) et propice au basculement.
Rappelez-vous, la loi de Lorentz et la règle des trois doigts :
Un champ perpendiculaire à un courant provoque l'apparition d'une force elle-même perpendiculaire au courant et au champ. Cette force est orientée dans une direction que l'on peut retrouver facilement à l'aide de la règle des trois doigts (ou du bonhomme d'Ampère) : dans le cas présent, on regarde un proton, donc une charge positive, il faut donc inverser la main que l'on regarde ... donc pour la main gauche, le pouce = B1, l'index =\(\mu\) et le majeur = F.
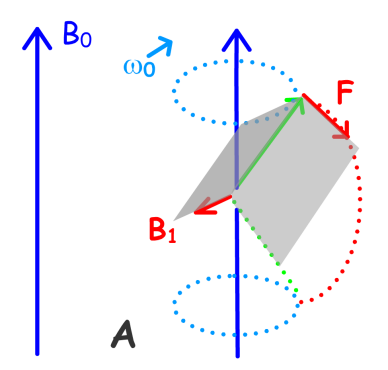
Quand il y a précession, nous avons vu que le vecteur moment magnétique \(\mu\) décrit un cône autour de l'axe du champ magnétique Bo à la fréquence \(\nu_o=\frac{\omega}{2\pi}\).
Si on applique le même champ fixe B1 on observera les conditions de basculement décrites précédemment uniquement lors du passage du moment magnétique \(\mu\) dans la position propice à ce basculement. C'est ce que l'on peut observer dans la situation notée A.
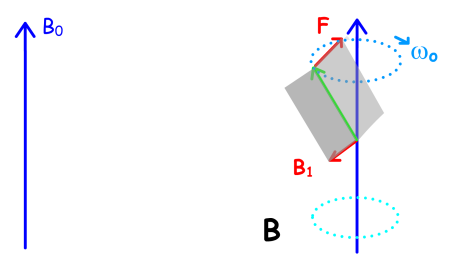
Par contre, le champ B1 étant de direction fixe, il ne sera plus propice au basculement pour d'autres positions du vecteur moment magnétique vis à vis du vecteur B1.
Le basculement sera alors compromis puisque la force peut tendre à s'opposer à ce mouvement. C'est le cas illustré en B. Le vecteur moment magnétique effectuant un mouvement de précession, pour observer tout le temps les conditions de basculement, il faudrait donc appliquer également un champ B1 tournant à la même vitesse de rotation.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Pour observer le basculement des vecteurs moments magnétiques et observer ainsi la transition entre les niveaux d'énergie, il faut donc appliquer un champ B1 tournant à la même fréquence que la fréquence de rotation des moments magnétiques \(\mu\) à savoir la fréquence de Larmor.
On a \(\omega o=\omega\) et donc \(\omega o= 2\pi.\nu = \gamma.Bo = \omega o\)
\(2.\pi.\nu =\gamma.Bo\) est la formule fondamentale de la RMN. \(\nu\) est la radiofréquence, \(\gamma\) dépend du type de noyau.
L'explication du nom de la technique : R.M.N.
Les deux fréquences étant égales, il y a Résonance, le phénomène étant consacré à l'observation des propriétés magnétiques du noyau, on parle donc de Résonance Magnétique Nucléaire.
Nous venons de voir ce qui se passe à l'échelle microscopique, c'est-à-dire ce qui se passe pour le spin d'UN noyau... Voyons ce que l'on observe pour une collection de noyaux de même type, c'est-à-dire à l'échelle macroscopique.