Aspects macroscopiques
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Pour l'obtention d'un spectre on observe le comportement d'un grand nombre de molécules (0,5 à 1 cm3 de solution). A l'échelle macroscopique, ce n'est pas un spin que l'on observe mais une collection de spins. On l'a vu, une majorité d'entre eux est dans un état énergétique m = +\(\frac{1}{2}\) (le plus stable) et les autres sont dans l'état m = -\(\frac{1}{2}\).
Si l'on regroupe en un point l'ensemble de ces moments magnétiques on observe deux cônes de moments magnétiques de spin \(\mu\) qui précessionnent à la fréquence de Larmor, et qui, sous l'action du champ tournant B basculent sans discontinuer entre les deux états m = +\(\frac{1}{2}\) et m = -\(\frac{1}{2}\).
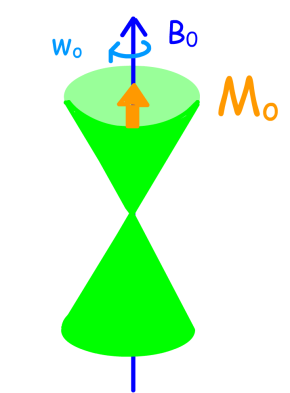
Finalement on observe deux cônes de moments magnétiques de spin \(\mu\) . L'état énergétique m = +\(\frac{1}{2}\) étant prépondérant, par rapport à l'état énergétique m = -\(\frac{1}{2}\) (moins peuplé), la magnétisation macroscopique Mo qui est la résultante des moments magnétiques de spins individuels m peut être représentée par le vecteur Mo.
Le vecteur Mo est un objet de la physique classique auquel s'appliquent les lois habituelles de l'électromagnétisme (de la même façon, l'intensité I d'un courant électrique représente le flux des quanta d'électricité, c'est-à-dire des électrons).
Cette magnétisation macroscopique Mo résultante est fonction de la différence de population des états quantiques magnétiques, elle-même étant dépendante de \(\Delta E\), la différence d'énergie entre les états m = -\(\frac{1}{2}\) et m = +\(\frac{1}{2}\). La différence d'énergie \(\Delta E\) est proportionnelle à l'induction Bo appliquée, à la température... et dépend de la nature du noyau étudié représenté par une constante \(\gamma\) (rapport gyromagnétique). On a \(\Delta E= (\frac{h}{2\pi}).\gamma.Bo\) avec h : constante de Planck et \(\gamma\): rapport gyromagnétique.
La sensibilité de la RMN étant fonction de \(\Delta E\), on observera donc les noyaux d'autant mieux que Bo sera important (RMN à haut champ) et que le rapport gyromagnétique \(\gamma\) sera grand (ce qui est le cas pour \(\textrm{}^1\textrm H\) et \(\textrm{}^{19}\textrm F\))