R.M.N. impulsionnelle
Envisageons maintenant les effets de la résonance sur cette magnétisation Mo en appliquant classiquement la règle de Lorentz.
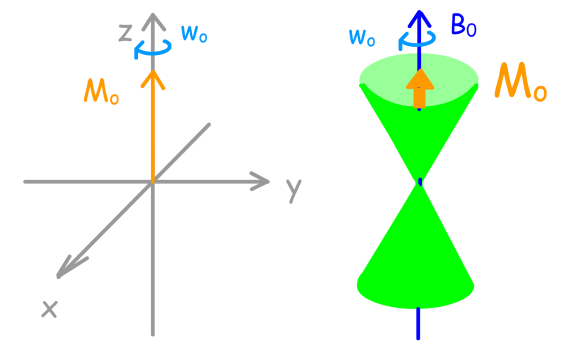
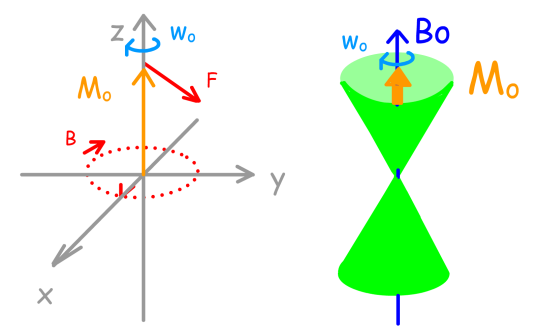
Sous l'action du champ B perpendiculaire à Bo et à Mo, la magnétisation macroscopique Mo va être soumise à une force F perpendiculaire à Mo et à B. Cette force F va faire basculer Mo autour de la direction de B et Mo va décrire un cercle autour de la direction de B, l'amenant, entre autres, à la valeur -Mo.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Cette situation est plus aisément traduite en se plaçant dans un référentiel tournant à wo (fréquence de Larmor) autour de l'axe z. Dans ce référentiel x'y'z', Mo se situe sur l'axe z' (tout comme Bo). Dans ce cas, Mo se situe sur l'axe z' (comme Bo) et le champ B sur l'axe x'.
Comme le référentiel x'y'z' tourne à la vitesse angulaire wo, B reste fixe dans ce référentiel.Sous l'action de B, il en résulte toujours une force F qui conduit Mo à entamer une rotation dans le plan z'y' autour de B. En supposant que le champ B soit appliqué suffisament longtemps, cette force F va provoquer un basculement complet de Mo vers le bas puis si le champ B est maintenu un nouveau basculement vers le haut... B va retrouver sa position initiale... et ainsi de suite...
Si B est maintenu indéfiniment, on voit donc que Mo va décrire un cercle dans le plan z'y' perpendiculaire au champ B.
Nous avons vu que si le champ B était maintenu constant indéfiniment, alors la magnétisation macroscopique Mo entamait une rotation autour du champ B avec une vitesse angulaire \(\omega= \gamma.B\), avec \(\gamma\) rapport gyromagnétique du noyau. En fait, le champ B n'est pas maintenu constant indéfiniment, mais agit seulement une fraction de seconde to (quelques micro secondes ou 10-6 s) et ainsi, le vecteur Mo ne bascule pas entièrement mais uniquement d'un angle \(\theta\). Comme il est possible de gérer facilement le temps de l'impulsion to , il est donc facile de connaître l'angle \(\theta\) puisque l'on a la relation \(\theta= \omega.t_o\), comme \(\omega=\gamma.B\), on obtient \(\theta=\gamma .B.t_o\) ...
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
On peut ainsi envisager un basculement de \(\theta= \frac{\pi}{2}\). Comme \theta= \omega.B.t... on aura\( \frac{t_\pi}{2} = \frac{\pi}{2.\gamma.B}\) ...et dans ce cas, l'excès de population est dans le plan x'y'.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
On peut également envisager un basculement de \(\theta=\pi\) .
Comme \(\theta= \omega.B.t\) ... on aura \(t_\pi = \frac{\pi}{\gamma.B}\) ... La rotation de M étant un mouvement circulaire uniforme, on voit que \(t_\pi =\frac{2.t_\pi}{2}\). Donc, pour une durée de mise en oeuvre de B deux fois plus grande que celle conduisant à l'excès de magnétisation dans le plan x'y', on obtient un basculement complet de Mo sous forme de -Mo. On a alors inversé la population de Boltzmann. Cette possibilité de gestion de l'angle de basculement de Mo est décisive dans la RMN moderne. Le temps de mise en oeuvre de B correspond à une impulsion de courte durée dans un émetteur de radiofréquence. D'où la qualification de RMN impulsionnelle ou RMN "pulsée" (de "pulse" en anglais).