Position la plus probable pour l'orbitale 2px
Durée : 20 mn
Note maximale : 5
Question
L'expression de l'orbitale \(2\textrm{px}\)est :
\(\Psi_{2p_{x}}(r,\theta,\varphi) = \frac{1}{4\sqrt{2\pi}}\bigg(\frac{Z}{\textrm{a}_{0}}\bigg)^{3/2} \frac{Z~r}{\textrm{a}_{0}}\exp(-Z~r/2\textrm{a}_{0})\sin\theta\cos\varphi\)
1. Suivant quelles directions de l'espace la densité volumique de probabilité associée à cette orbitale est-elle maximale ?
2. Quelles sont les positions les plus probables pour cette orbitale ?
Solution
1. Les directions suivant lesquelles la densité est maximale sont données pour \(\sin\theta = 1\) et \(\cos\varphi = 1\) .
Soit\(\theta = \pi/2\)et\(\varphi = 0\)ou\(\pi\). Ces relations définissent les directions Ox et Ox'.
Les positions les plus probables correspondent au maximum de la densité volumique\( \left \arrowvert \Psi_{2p_{x}}\right\arrowvert^{2}\).
Sur l'axe x'Ox, on peut écrire :
\(\bigg\arrowvert\Psi_{2p_{x}}\bigg\arrowvert^{2} = A~r^{2} \exp\big(-Zr/\textrm{a}_0)\)
\(\frac{ \partial \bigg\arrowvert\Psi_{2p_{x}}\bigg\arrowvert^{2}}{ \partial r} = A \bigg(2r - \frac{Zr^{2}}{\textrm{a}_{0}}\bigg)\exp( - Zr / \textrm{a}_{0}\big) = A~r~\bigg(2 - \frac{Zr}{\textrm{a}_{0}}\bigg)\exp\big(-Zr/\textrm{a}_0)\)
La dérivée s'annule en \(r = 0\), \(r = 2\textrm{a}_{0} /Z\) et à l'infini.
En \(r = 0\) et \(r =+ \infty\), la densité s'annule ; le maximum est donc\(r = 2\textrm{a}_{0} /Z\).
On obtient donc deux maxima en :
\(r = 2\textrm{a}_{0} /Z\), \(\theta = \pi/2\), \(\varphi = 0\) (direction Ox)
\(r = 2\textrm{a}_{0} /Z\), \(\theta = \pi/2\), \(\varphi = \pi\) (direction Ox')
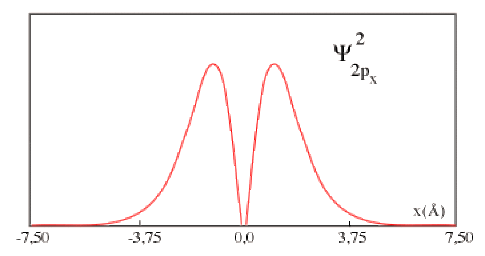
\(\bigg\arrowvert\Psi_{2p_{x}}\bigg\arrowvert^{2}\)le long de l'axe x'Ox