Limite d'une suite
Le concept de limite se dégage de la proposition suivante :
Proposition :
Si \((u_n)\) est une suite réelle convergente il existe un réel \(l\) unique tel que \((u_n)\) converge vers \(l\) quand \(n\) tend vers \(+\infty\).
Preuve :
Il s'agit d'une démonstration par l'absurde.
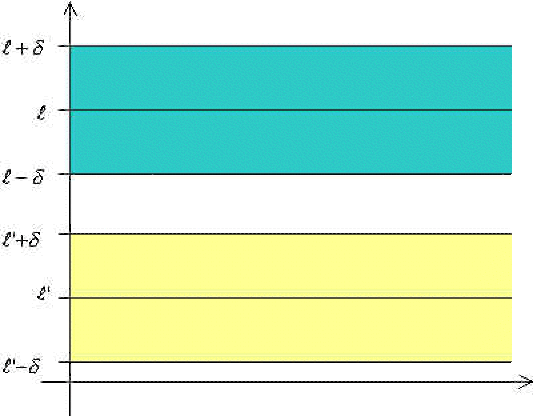
On suppose qu'il existe deux réels distincts \(l\) et \(l'\) tels que \((u_n)\) converge vers \(l\) et \((u_n)\) converge vers \(l'\).
Deux intervalles ouverts centrés respectivement en \(l\) et \(l'\) et disjoints (par exemple \(\displaystyle{]l-\delta,l+\delta[}\) et \(\displaystyle{]l'-\delta,l'+\delta[}\) avec \(\displaystyle{\delta=\frac{\vert l-l'\vert}{3}}\)) ne peuvent contenir tous les termes de la suite à partir d'un certain rang.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
L'unicité du réel \(l\) étant ainsi établie on peut lier \(l\) et \((u_n)\).
Définition :
Si \((u_n)\) est une suite convergente, l'unique réel \(l\) , tel que \((u_n)\) converge vers \(l\) , s'appelle la limite de la suite \((u_n)\) et se note \(\displaystyle{\lim_{n\to+\infty}u_n}\).
On notera désormais \(\displaystyle{l=\lim_{n\to+\infty}u_n}\) et on dira que la suite \((u_n)\) est convergente et a pour limite \(l\) , plutôt que la suite \((u_n)\) converge vers \(l\).
Attention :
On utilisera le symbole \(\displaystyle{\lim_{n\to+\infty}u_n}\), seulement quand la convergence de la suite a été établie.
Remarque :
Ces remarques portent sur la densité de \(\mathbb Q\) dans \(\mathbb R\) et sur la vitesse de convergence.
Soient les suites \(\displaystyle{\left(\frac{1}{n}\right)_{n\geq 1},\left(\frac{1}{n+(-1)^n\sqrt n}\right)_{n\geq 2}}\)
et pour tout \(x\) réel la suite \((x_n)\) des approximations décimales par défaut d'ordre \(n\) converge vers \(x\), des exemples du paragraphe précédent.
Les suites \(\displaystyle{\left(\frac{1}{n}\right)_{n\geq 1},\left(\frac{1}{n+(-1)^n\sqrt n}\right)_{n\geq 2}}\) sont convergentes et ont pour limite 0.
Pour tout réel \(x\), la suite \((x_n)\) de rationnels constituée par ses approximations décimales par défaut est convergente et a pour pour limite \(x\). On a donc montré ainsi: Tout réel est limite d'une suite de rationnels et même de décimaux.
On retrouve la propriété : \(\mathbb Q\) est dense dans \(\mathbb R\) (il s'agit d'une définition équivalente de la notion de densité cf cours sur les réels).
On remarque, sur ces exemples, que l'entier \(N(\epsilon)\) varie, pour \(\epsilon=10^{-2}\) de 2 à 201. La connaissance de \(N(\epsilon)\) permet d'avoir une idée de la vitesse de convergence de la suite.
On remarque également que l'on approche des nombres irrationnels comme \(\sqrt2,\pi , \ln 2\) avec la précision souhaitée grâce à des suites de rationnels.
Un bon algorithme est un algorithme qui "donne" beaucoup de décimales à chaque opération, ainsi la suite \(\mathcal U\) définie par \({\left\{\begin{array}{ll}u_0=2, &\\u_{n+1}=\frac{1}{u_n}+\frac{u_n}{2} & \forall n\in\mathbb N\end{array}\right.}\), est convergente et a pour limite \(\sqrt2\) et le passage de \(u_n\) à \(u_{n+1}\) conduit à un doublement du nombre des décimales exactes; en effet les inégalités :
\(\displaystyle{0< u_{n+1}-\sqrt2=\frac{(u_n-\sqrt2)^2}{2u_n}<\frac{(u_n-\sqrt2)^2}{2}}\)
entraînent que, si l'on a \(0< u_n-\sqrt2<10^{-k}\), on en déduit \(\displaystyle{0< u_{n+1}-\sqrt2<10^{-2k}}\).