Suites tendant vers + l'infini ou - l'infini , suites sautantes
Parmi les suites divergentes, les suites qui tendent vers \(\displaystyle{+\infty}\) ou \(\displaystyle{(-\infty)}\) jouent un rôle particulier.
Leur comportement, dans certains cas, s'apparente à celui des suites convergentes.
Intuitivement la suite \((u_n)\) tend vers \(+\infty\) si \(u_n\) est grand positif pour \(n\) grand.
Définition : Suite tendant vers + l'infini
Soit \((u_n)\) une suite réelle ; on dit que \((u_n)\) tend vers \(+\infty\) quand \(n\) tend vers \(+\infty\) si quelque soit le réel \(A\) il existe un entier \(N\) tel que \(n\geq N\) entraîne \(u_n>A\).
Formellement on écrit :
\(\displaystyle{\forall A\in\mathbb R,\exists N\in\mathbb N,\forall n\in\mathbb N}\) \(\displaystyle{(n\geq N\Rightarrow u_n> A)}\)
Notation
On note \(u_n \to+\infty\) ou encore \(\displaystyle{\lim_{n\to+\infty}u_n=+\infty}\), tout en remarquant l'ambiguité de cette notation, car une suite qui tend vers \(+\infty\) n'est pas convergente et il est préférable de réserver le symbole lim pour les suites convergentes.
On définit de façon analogue les suites qui tendent vers \(-\infty\). On remarque que, dans la définition, l'inégalité \(u_n>A\) s'interprète comme l'appartenance de \(u_n\) à un voisinage de \(+\infty\).
Les représentations
La définition exprime:
en représentation axiale qu'il n'existe qu'un nombre fini de termes en dehors de l'intervalle \(]A,+\infty[\), ou encore tous les \(u_n\) pour \(n\geq \mathbb N\) appartiennent à l'intervalle \(]A,+\infty[\),
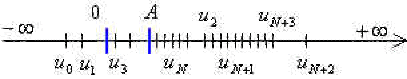
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
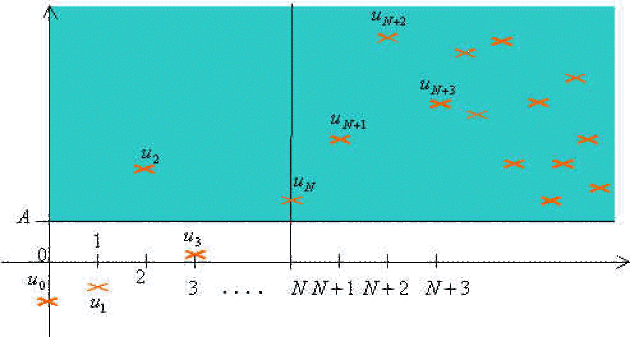
en représentation graphique qu'il n'existe qu'un nombre fini de points \((n,u_n)\) en dehors de la bande \(N\times]A,+\infty[\) encore que tous les points \((n,u_n)\) pour \(n\geq N\) appartiennent à la bande \(N\times]A,+\infty[\).
Parmi les suites divergentes, le comportement des suites qui tendent vers \(+\infty\) ou \(-\infty\) est très différent de celui des suites comme \(\Big((-1)^n\Big)\) ou \(\displaystyle{\Big(n\sin\frac{n\pi}{2}\Big)}\) (suites "sautantes") que l'on définit plus précisément de la façon suivante :
Définition : Suite sautante
On dit qu'une suite \((u_n)\) est une suite sautante s'il existe des réels \(a\) et \(b\) \((a< b)\) tels que
\(u_n< a\) pour une infinité de valeurs de \(n\),
\(u_n> b\) pour une infinité de valeurs de \(n\).
Les représentations
Cela s'exprime :
en représentation axiale :
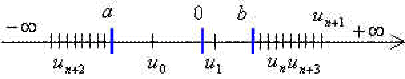
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
en représentation graphique :
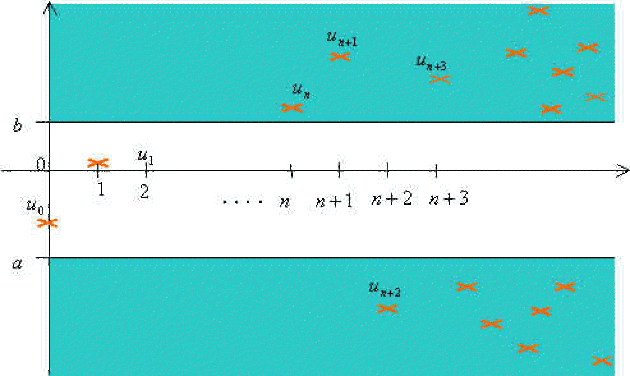
Pour la suite \(\Big((-1)^n\Big)\) on prend par exemple \(a=-\frac{1}{2}\) et \(b=\frac{1}{2}\), pour la suite \(\displaystyle{\Big(n\sin\frac{n\pi}{2}\Big)}\), \(a=-1\) et \(b=1\).
On montre que pour une suite divergente trois cas sont possibles :
\(u_n\to+\infty\)
\(u_n\to-\infty\)
\((u_n)\) est une suite sautante.