Introduction
Soient \(E\) et \(\mathcal F\) deux \(\mathbf K\)-espaces vectoriels de type fini, \(\mathcal B_E\) et \(\mathcal B'_E\) deux bases de \(E,\mathcal B_F\) et \(\mathcal B'_F\) deux bases de \(\mathcal F\). Soit \(\phi\) une application linéaire de \(E\) dans \(\mathcal F\).
L'objet de ce paragraphe est d'établir une relation entre les matrices associées à \(\phi\) par rapport, d'une part aux bases \(\mathcal B_E\) et \(\mathcal B_F\) d'autre part aux bases \(\mathcal B'_E \)et \(\mathcal B'_F\) , autrement dit entre \([\phi]_{\mathcal B_E}^{\mathcal B_F}\) et \([\phi]_{\mathcal B'_E}^{\mathcal B'_F}\).
En s'inspirant de l'interprétation qui a été donnée de la matrice de passage d'une base à une autre, on introduit l'application identique de \(E\) et l'application identique de \(\mathcal F\) et on considère le composé \(\mathcal Id_F\circ\phi\circ\mathcal Id_E\) selon le schéma suivant
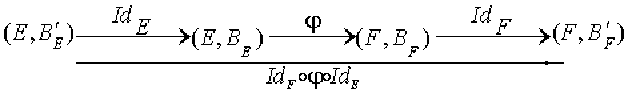
Alors \([\mathcal Id_F\circ\phi\circ\mathcal Id_E]_{\mathcal B'_E}^{\mathcal B'_F}=[\mathcal Id_F]_{\mathcal B_F}^{\mathcal B'_F}[\phi]_{\mathcal B_E}^{\mathcal B_F}[\mathcal Id_E]_{\mathcal B'_E}^{\mathcal B_E}\)
Or la matrice de l'identité de\( E\) avec\( \mathcal B'_E\) comme base de départ et \(\mathcal B_E\) comme base de l'espace d'arrivée est la matrice de passage de \(\mathcal B_E\) à \(\mathcal B'_E\).
De même, la matrice de l'identité de\( \mathcal F\) avec \(\mathcal B_F\) comme base de l'espace de départ et \(\mathcal B'_F\) comme base de l'espace d'arrivée est la matrice de passage de \(\mathcal B'_F\) à \(\mathcal B_F\), soit l'inverse de la matrice de passage de \(\mathcal B_F\) à \(\mathcal B'_F\) .
De plus, on a l'égalité : \(\mathcal Id_F\circ\phi\circ\mathcal Id_E=\phi\)
Cela permet d'énoncer la propriété suivante...