Caractérisation des matrices équivalentes par leur rang
On a vu que toutes les matrices associées à une même application linéaire ont même rang.
Ce résultat, et sa réciproque, vont être énoncés sous une autre forme en caractérisant les matrices associées à une même application linéaire.
Pour cela il est nécessaire de connaître les formules de changement de base et la notion de matrices équivalentes. Nous allons rappeler les résultats qui vont être utilisés.
Rappel :
Les principaux résultats ou définitions qui seront utilisés sont les suivants :
Résultat 1 : Formule de changement de bases
Soient\( E\) et \(\mathcal F\) deux\( \mathbf K\)-espaces vectoriels de type fini, \(\mathcal B_E\) et \(\mathcal B'_E\) deux bases de \(E\), et \(\mathcal B_F\) et \(\mathcal B'_F\) deux bases de \(\mathcal F\). Soit\( \phi\) une application linéaire de \(E\) dans \(\mathcal F\). Alors, la matrice associée à \(\phi\) par rapport aux bases \(\mathcal B_E\) et \(\mathcal B_F\), et la matrice associée à \(\phi\) par rapport aux bases \(\mathcal B'_E\) et \(\mathcal B'_F\) sont liées par la formule :
\(\displaystyle{[\phi]_{\mathcal B'_E}^{\mathcal B'_F}=\mathcal P_{\mathcal B'_F,\mathcal B_F}[\phi]_{\mathcal B_E}^{\mathcal B_F}\mathcal P_{\mathcal B_E,\mathcal B'_F}=(\mathcal P_{\mathcal B_F,\mathcal B'_F})^{-1}[\phi]_{\mathcal B_E}^{\mathcal B_F}\mathcal P_{\mathcal B_E,\mathcal B'_E}}\)
Rappel de la notation : Si \(\mathcal B\) et \(\mathcal B'\) sont des bases d'un même espace vectoriel \(\mathcal G,\mathcal P_{\mathcal B,\mathcal B'}\) est la matrice de passage de la base\( \mathcal B\) à la base \(\mathcal B'\). Définition : Deux matrices \(\mathcal A\) et \(\mathcal B\) de \(\mathcal M_{n,p}(\mathbf K)\) sont équivalentes s'il existe une matrice \(\mathcal P\) carrée d'ordre \(p\), inversible et une matrice\( \mathcal R\) carrée d'ordre \(n\), inversible telles que \(\mathcal B=\mathcal{RAP}\).
Résultat 2 :
Soit \(\mathcal M\) une matrice carrée d'ordre \(n\) inversible. Étant donnée une base \(\mathcal B\) de \(\mathbf K^n\), il existe une unique base \(\mathcal B'\) de \(\mathbf K^n\) telle que\( \mathcal M\) soit la matrice de passage de \(\mathcal B\) à \(\mathcal B'\).
Conséquences des résultats 1 et 2 :
Multiplier à droite la matrice d'une application linéaire par une matrice inversible revient à changer de base sur l'espace de départ. Donc les matrices\( \mathcal A\) et \(\mathcal{AP}\), avec \(\mathcal P\) inversible, peuvent être considérées comme les matrices d'une même application linéaire avec deux bases différentes sur l'espace de départ et la même base sur l'espace d'arrivée.
De même, multiplier à gauche la matrice d'une application linéaire par une matrice inversible revient à changer de base sur l'espace d'arrivée. Donc les matrices \(\mathcal A\) et\( \mathcal{PA}\), avec \(\mathcal P\) inversible, peuvent être considérées comme les matrices d'une même application linéaire avec deux bases différentes sur l'espace d'arrivée et la même base sur l'espace de départ.
Cela conduit au résultat suivant :
Résultat 3 :
Deux matrices sont associées à une même application linéaire si et seulement si elles sont équivalentes.
Démonstration : Résultat 1 : Formule de changement de bases
Soient \(E\) et \(\mathcal F\) deux \(\mathbf K\)-espaces vectoriels de type fini, \(\mathcal B_E\) et \(\mathcal B'_E\) deux bases de \(E\), \(\mathcal B_F\) et \(\mathcal B'_F\) et deux bases de \(\mathcal F\). Soit\( \phi\) une application linéaire de \(E\) dans\( \mathcal F\). Alors, la matrice associée à \(\phi\) par rapport aux bases\( \mathcal B_E\) et \(\mathcal B_F\), et la matrice associée à \(\phi\) par rapport aux bases \(\mathcal B'_E\) et \(\mathcal B'_F\) sont liées par la formule :
\(\displaystyle{[\phi]_{\mathcal B'_E}^{\mathcal B'_F}=\mathcal P_{\mathcal B'_F,\mathcal B_F}[\phi]_{\mathcal B_E}^{\mathcal B_F}\mathcal P_{\mathcal B_E,\mathcal B'_F}=(\mathcal P_{\mathcal B_F,\mathcal B'_F})^{-1}[\phi]_{\mathcal B_E}^{\mathcal B_F}\mathcal P_{\mathcal B_E,\mathcal B'_E}}\)
Preuve :
Soient \(E\) et \(\mathcal F\) deux \(\mathbf K\)-espaces vectoriels de type fini,\( \mathcal B_E\) et \(\mathcal B'_E\) deux bases de \(E,_mathcalB_F\) et \(\mathcal B'_F\) deux bases de \(\mathcal F\).
Soit \(\phi\) une application linéaire de \(E\) dans \(\mathcal F\).
Il s'agit d'établir une relation entre les matrices associées à \(\phi\) par rapport, d'une part aux bases \(\mathcal B_E\) et \(\mathcal B_F\) et d'autre part aux bases \(\mathcal B'_E\) et \(\mathcal B'_F\), autrement dit entre \([\phi]_{\mathcal B_E}^{\mathcal B_F}\) et \([\phi]_{\mathcal B'_E}^{\mathcal B'_F}\).
En utilisant, pour les deux espaces concernés, l'interprétation de la matrice de passage d'une base à une autre, en termes de matrice associée à l'application identique par rapport à des bases bien choisies, on a le schéma suivant
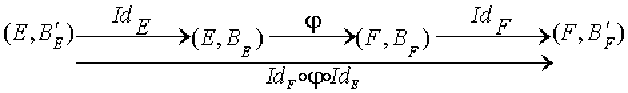
Sa traduction matricielle est
\([\mathcal Id_F\circ\phi\circ\mathcal Id_E]_{\mathcal B'_E}^{\mathcal B'_F}=[\mathcal Id_F]_{\mathcal B_F}^{\mathcal B'_F}[\phi]_{\mathcal B_E}^{\mathcal B_F}[\mathcal Id_E]_{\mathcal B'_E}^{\mathcal B_E}\).
Or la matrice de l'identité de \(E\) avec \(\mathcal B'_E\) comme base de départ et \(\mathcal B_E\) comme base de l'espace d'arrivée est la matrice de passage de \(\mathcal B_E\) à \(\mathcal B'_E\), notée \(\mathcal P_{\mathcal B_E,\mathcal B'_E}\). De même, la matrice de l'identité de \(\mathcal F\) avec \(\mathcal B_F\) comme base de l'espace de départ et \(\mathcal B'_F\) comme base de l'espace d'arrivée est la matrice de passage de \(\mathcal B'_F\) à \(\mathcal B_F\), soit l'inverse de la matrice de passage de \(\mathcal B_F\) à \(\mathcal B'_F\).
De plus, on a l'égalité :\(\mathcal Id_F\circ\phi\circ\mathcal Id_E=\phi\).
Démonstration : Résultat 2 : Interprétation d'une matrice carrée inversible comme la matrice de passage d'une base à une autre
Soit \(\mathcal M\) une matrice carrée d'ordre \(n\) inversible. Étant donnée une base \(\mathcal B\) de\( \mathbf K^n\) , il existe une unique base \(\mathcal B'\) de \(\mathbf K^n\) telle que \(\mathcal M\) soit la matrice de passage de \(\mathcal B\) à \(\mathcal B'\).
Preuve :
Soit \(\mathcal B=(e_1,e_2,\cdots,e_n)\) une base donnée de \(\mathbf K^n\) et soit \(\psi\) l'endomorphisme de \(\mathbf K^n\) dont la matrice par rapport à la base \(\mathcal B\) (sur l'espace de départ et d'arrivée) est égale à \(\mathcal M\), soit \([\psi]_{\mathcal B}\).
Comme \(\mathcal M\) est inversible, \(\psi\) aussi, c'est donc une bijection. Les vecteurs\( \psi(e_1),\psi(e_2),\cdots,\psi(e_n)\) images par un automorphisme d'une base de \(\mathbf K^n\), déterminent donc une base.
Il vient alors la proposition suivante :
Proposition :
Si deux matrices sont équivalentes, alors elles ont le même rang.
Cela découle immédiatement du résultat \(3\) et du théorème liant le rang d'une application linéaire et d'une matrice associée.