Modèle de matrice de rang r
L'objet de ce paragraphe est de montrer la propriété réciproque c'est-à-dire de montrer que toutes les matrices d'un type donné ayant le même rang sont équivalentes à une même matrice. Cela prouvera que toutes les matrices de même type qui ont le même rang sont équivalentes. Les preuves sont essentiellement basées sur l'interprétation d'une matrice en termes d'application linéaire.
Ce même résultat peut être obtenu par un calcul purement matriciel en utilisant les transformations élémentaires sur les matrices. Cet aspect est traité dans la quatrième partie.
Ce résultat est extrêmement utile car, par exemple, il permet de démontrer par des procédés élémentaires (en particulier sans utiliser la théorie de la dualité) qu'une matrice et sa transposée ont le même rang.
Théorème : "Modèle" des matrices de rang r
Soit\( p\) et \(n\) des entiers supérieurs ou égaux à \(1\). Soit \(r\) un entier supérieur à \(1\) et inférieur ou égal à \(p\) et à \(n\). Une matrice non nulle de\( \mathcal M_{n,p}(\mathbf K)\) est de rang \(r\) si et seulement si elle est équivalente à la matrice \(\mathcal M_{r,n,p}\) de \(\mathcal M_{n,p}\mathbf K\) définie par :
\(\mathcal M_{r,n,p}=\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\)
Explicitation des notations
\(\mathcal I_r\) désigne la matrice unité d'ordre \(r\).\( \mathcal O_{s,t}\) désigne la matrices nulle à \(s\) lignes et \(t\) colonnes.
Preuve :
1) Soit \(r\) un entier supérieur ou égal à \(1\) et inférieur ou égal à \(p\) et à \(n\),
et la matrice \(\mathcal M_{r,n,p}=\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\) de \(\mathcal M_{n,p}\mathbf K\).
Les \(p-r\) dernières colonnes de \(\mathcal M_{r,n,p}\) étant nulles, le sous espace de \(\mathbf K^n\) engendré par les vecteurs colonnes de la matrice \(\mathcal M_{r,n,p}\) est égal au sous-espace engendré par les \(r\) premiers vecteurs colonnes de cette matrice. Or ces vecteurs sont les \(r\) premiers vecteurs de la base canonique de l'espace\( \mathbf K^n\), donc ils sont linéairement indépendants. Le sous-espace engendré par les vecteurs colonnes de la matrice \(\mathcal M_{r,n,p}\) est donc de dimension \(r\) et par conséquent le rang de \(\mathcal M_{r,n,p}\) est égal à \(r\). Comme deux matrices équivalentes ont même rang, toute matrice équivalente à la matrice \(\mathcal M_{r,n,p}\) est de rang \(r\).
2) Réciproque :
Soit \(\mathcal M\) une matrice de \(\mathcal M_{n,p}(\mathbf K)\) de rang \(r\) où \(r\) est un entier supérieur à\( 1\) et inférieur ou égal à \(p\) et à \(n\). Il s'agit de démontrer que \(\mathcal M\) est équivalente à \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\). La démonstration utilise une application linéaire associée à \(\mathcal M\).
Rappel : Construction d'une application linéaire associée à une matrice
Soit \(\mathcal M\) un élément de \(\mathcal M_{n,p}(\mathbf K)\). Il existe des espaces vectoriels \(E\) et \(\mathcal F\) sur \(\mathbf K\), des bases \(\mathcal B_E\) et \(\mathcal B_F\) sur\( E\) et \(\mathcal F\) respectivement et une application linéaire \(\psi\) de\( E\) dans \(\mathcal F\) tels que \(\mathcal M=\mathcal M(\psi,\mathcal B_E,\mathcal B_F)\) .
Les choix (canoniques) successifs suivants sont effectués :
Les espaces vectoriels
Nécessairement l'espace de départ a pour dimension le nombre de colonnes de la matrice soit \(p\) ; l'espace d'arrivée a pour dimension le nombre de lignes de la matrice soit \(n\). On choisit \(E=\mathbf K^p,\mathcal F=\mathbf K^n\) .
Les bases
De manière naturelle, on choisit les bases canoniques sur chacun de ces espaces. On les notera \(\mathcal B_{\mathbf K^p}\) et \(\mathcal B_{\mathbf K^n}\).
Une application linéaire
C'est l'application linéaire \(\psi\) de \(E=\mathbf K^p\) dans \(\mathcal F=\mathbf K^n\) dont la matrice par rapport aux bases canoniques est égale à \(\mathcal M\).
Soit donc \(f\) l'application linéaire de \(\mathbf K^p\) dans \(\mathbf K^n\) dont la matrice relativement aux bases canoniques de \(\mathbf K^p\) et \(\mathbf K^n\) est égale à \(\mathcal M\). Comme \(\mathcal M\) est non nulle (son rang est supérieur ou égal à \(1\)) l'application linéaire\( f\) est aussi non nulle.
Pour obtenir le résultat souhaité, il suffit, en vertu des résultats rappelés au début de ce paragraphe, de construire une base de et une base \(\mathcal K^n\) de par rapport auxquelles la matrice associée à \(f\) soit égale à \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\).
Propriété : Propriétés de f
Comme \(\mathcal M\) est de rang \(r\), l'application linéaire\( f\) est aussi de rang \(r\), ce qui signifie que son image est un sous-espace vectoriel de dimension \(r\) de \(\mathbf K^n\).
D'après le théorème du rang, le noyau de\( f\) est un sous espace vectoriel de dimension \(p-r\) de\( \mathbf K^p\). Ces remarques permettent de faire les constructions suivantes :
Construction d'une base de Kp
Soit \((\epsilon_{r+1},\epsilon_{r+2},\cdots,\epsilon_{p})\) une base de Kerf. La famille de vecteurs \(\epsilon_{r+1},\epsilon_{r+2},\cdots,\epsilon_{p}\) étant libre, les hypothèses du théorème de la base incomplète sont satisfaites.
Il existe donc \(r=p-(p-r)\) vecteurs, notés \(\epsilon_{1},\epsilon_{2},\cdots,\epsilon_{r}\)
tels que \(\mathcal B=(\epsilon_1,\epsilon_2,\cdots,\epsilon_r,\epsilon_{r+1},\epsilon_{r+2},\cdots,\epsilon_p)\) soit une base de \(\mathbf K^p\) .
Par conséquent, quelle que soit la base que l'on choisit sur \(\mathbf K^n\), la matrice associée à \(f\) en prenant \(\mathcal B\) comme base de \(\mathbf K^p\) a ses \(p-r\) dernières colonnes nulles car on a :
\(\forall i,r+1\leq i\leq p,f(\epsilon_i)=0\).
Il suffit donc de déterminer une base de \(\mathbf K^n\) permettant d'obtenir les \(r\) premières colonnes de la forme voulue pour achever la démonstration.
Construction d'une base de Kn
L'image de \(f\) est engendrée par les images par \(f\) des vecteurs d'une base de \(\mathbf K^p\), par exemple \(\mathcal B\). Donc les vecteurs
\(f(\epsilon_1),f(\epsilon_2),\cdots,f(\epsilon_r),f(\epsilon_{r+1}),f(\epsilon_{r+2}),\cdots,f(\epsilon_{p})\)
engendrent l'image de \(f\).
Puisque les \(p-r\) derniers vecteurs sont nuls, les r vecteurs \(f(\epsilon_1),f(\epsilon_2),\cdots,f(\epsilon_{p})\) engendrent l'image de \(f\). Or cette image est de dimension \(r\). Donc \(f(\epsilon_1),f(\epsilon_2),\cdots,f(\epsilon_{p})\) est une base de l'image de \(f\). D'après le théorème de la base incomplète, il existe\( n-r\) vecteurs \(\mathcal V_{r+1},\mathcal V_{r+2},\cdots,\mathcal V_{n}\) de \(\mathbf K^n\) tels que \((f(\epsilon_1),f(\epsilon_2),\cdots,f(\epsilon_r),\mathcal V_{r+1},\mathcal V_{r+2},\cdots,\mathcal V_{n})\) soit une base, notée \(\mathcal C\) de \(\mathbf K^n\).
Conclusion
Alors, la matrice associée à \(f\) en prenant \(\mathcal B\) comme base de \(\mathbf K^p\) et \(\mathcal C\) comme base de \(\mathbf K^n\), est égale à \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\).
Remarque : Remarque 1
Le théorème de la base incomplète joue un rôle fondamental dans cette démonstration
Remarque : Remarque 2
Cette démonstration est très élégante et relativement simple. En effet elle ne fait intervenir que des théorèmes très classiques et fondamentaux sur les espaces vectoriels de type fini et sur les applications linéaires. Toutefois, elle présente l'inconvénient de ne pas être effective : en effet l'existence des bases \(\mathcal B\) et \(\mathcal C\) a été démontrée, mais le procédé ne nous donne pas une construction pratique de ces bases. En langage matriciel, cette démonstration ne nous donne pas d'expression explicite des matrices \(\mathcal R\) et \(\mathcal P\) inversibles, telles que
\(\mathcal M=\mathcal P\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\mathcal R\)
Il existe une démonstration de ce résultat utilisant les transformations élémentaires, plus lourde car calculatoire, mais qui donne des valeurs explicites de\( \mathcal R\) et \(\mathcal P\). Cette démonstration est étudiée dans la quatrième partie.
Caractérisation des matrices de même rang
L'ensemble des résultats précédents est résumé par le théorème
Théorème : Rang et matrices équivalentes
Deux matrices de même type ont le même rang si et seulement si elle sont équivalentes.
Cette propriété permet de trouver, par des moyens relativement élémentaires, le rang de la matrice transposée d'une matrice.
Théorème : Rang de la transposée d'une matrice
Soit \(\mathcal M\) une matrice de \(\mathcal M_{n,p}(\mathbf K)\). Les matrices \(\mathcal M\) et \({}^t\mathcal M\) ont même rang.
\(\textrm{rang}(\mathcal M)=\textrm{rang}({}^t\mathcal M)\)
Soit \(\mathcal M\) une matrice non nulle de \(\mathcal M_{n,p}(\mathbf K).\) Soit \(r\) son rang (donc \(r\) est supérieur ou égal à \(1\)). D'après le théorème précédent, \(\mathcal M\) est équivalente à la matrice \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\), ce qui signifie qu'il existe une matrice inversible\( \mathcal P\) appartenant à \(\mathcal M_n(\mathbf K)\) et une matrice inversible R appartenant à\( \mathcal M_p(\mathbf K)\) telles que \(\mathcal M=\mathcal P\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\mathcal R\).
Les règles de calcul sur la transposition des matrices permettent d'en déduire l'égalité :
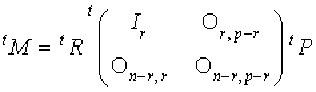
Or la matrice \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\) appartient à \(\mathcal M_{n,p}\mathbf K\) . Sa transposée appartient donc à et est égale à \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,n-r}\\\mathcal O_{p-r,r}&\mathcal O_{p-r,n-r}\end{array}\right)\). Bien faire attention à l'ordre des différents blocs dans cette matrice.
Donc l'égalité précédente devient :
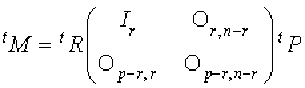
Or, comme \(\mathcal P\) (respectivement \(\mathcal R\)) est une matrice inversible \({}^t\mathcal P\), (respectivement \({}^t\mathcal R\)) est inversible. L'égalité précédente signifie donc que \({}^t\mathcal M\) est équivalente à la matrice \(\mathcal M_{r,p,n}\). C'est donc une matrice de rang \(r\).
Remarque : Destinée aux étudiants connaissant la théorie de la dualité
Il existe une démonstration de ce résultat faisant intervenir la notion de transposée d'une application linéaire.
Plus simple en apparence, elle fait cependant intervenir tous les concepts liés à la théorie de la dualité, ce qui la rend en fait plus complexe.
Comme les vecteurs lignes de \(\mathcal M\) sont les vecteurs colonnes de \({}^t\mathcal M\), on en déduit immédiatement le corollaire suivant :
Corollaire :
Soit \(\mathcal M\) une matrice de\( \mathcal M_{n,p}(\mathbf K)\). Alors le rang de \(\mathcal M\) est la dimension du sous-espace de \(\mathbf K^p\) engendré par les \(n\) vecteurs lignes de \(\mathcal M\).