Exercice 11
Partie
Question
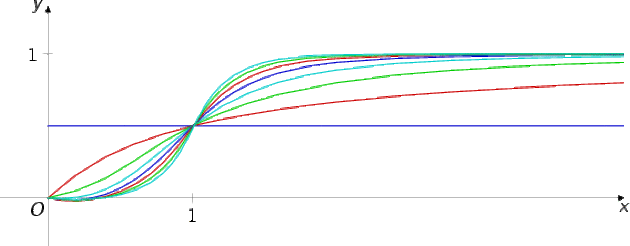
Soit la suite (\(f_n\)) de fonctions définies sur \(\mathbb{R_+}\) par \(f_n(x) = \frac{x^n}{1 + x^n}\)
Etudier la convergence simple de (\(f_n\)) sur \(\mathbb{R_+}\) .
Solution détaillée
0 \(\leqslant\) x < 1 :
alors \(\displaystyle \lim_{n \rightarrow +\infty} n^x = 0\) donc \(\displaystyle \lim_{n \rightarrow +\infty} f_n(x) = 0\)
x = 1 :
alors, pour tout n,\(f_n(1) = \frac{1}{2}\) donc \(\displaystyle \lim_{n \rightarrow +\infty} f_n(x) =\frac{1}{2}\)
1 < x :
alors \(f_n(x) = 1- \frac{1}{1 + x^n}\) et, comme \(\displaystyle \lim_{n \rightarrow +\infty} x^n = +\infty\) , on en déduit que \(\displaystyle \lim_{n \rightarrow +\infty} f_n(x) = 1\) .
La suite (\(f_n\)) converge simplement sur \(\mathbb{R_+}\) vers la fonction f définie par \(\left \{ \begin{array}{cc} 0 \leqslant x < 1& f(x)=0 \\ x=1 & f(x)= \frac{1}{2} \\ 1 <x& f(x)=1 \end{array} \right.\)