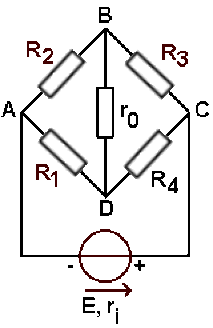
Pont de Wheatstone (1)
Partie
Question
Déterminer les intensités des courants :
1) dans la branche \(BD\)
2) dans la branche \(AC\)
Application numérique :
\(R_1 = R_2 = 300 \;\Omega ; R_3 = R_4 = 400\;\Omega\)
\(E = 20 \textrm{ V} ; r_i = 50 \;\Omega ; r_0 = 100 \;\Omega\)
Aide simple
Choisir un squelette excluant la (les) branche(s) étudiée(s).
Aide détaillée
Choisir les mailles de façon que la (les) branche(s) étudiée(s) soit (soient) parcourue(s) par un seul courant de maille.
Solution simple
\(I_{BD} = 0\)
\(I_{AC} = 50 \textrm{ mA}\)
Solution détaillée
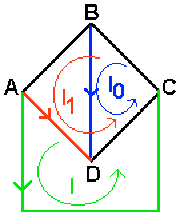
Le squelette doit passer par \(A, B, C, D\) et exclure les branches \(AC \textrm{ et }BD\) ; un choix possible est donc \(ABCD\) ; on obtient \(3\) mailles indépendantes en ajoutant \(BD, AD, AC\) ; les inconnues du problème sont alors les intensités \(I_0, I_1, I\) dans ces branches ; les autres branches sont parcourues par des courants qui sont la somme algébrique des courants des mailles auxquelles elles appartiennent.
Avec le choix indiqué sur la figure, la loi des mailles donne :
maille \(BDCB : - r_0.I_0 - R_4.(-I + I_0 + I_1) - R_3.(I_0+I_1) = 0\)
maille \(BADCB : -R_2.I_1 - R_1.(I_1 - I) - R_4.(-I + I_0 + I_1) - R_3.(I_0 + I_1) = 0\)
maille \(ACDA : E - r_i.I + R_4.(-I + I_0 + I_1) + R_1.(-I + I_1) = 0\)
Ce qui donne un système de \(3\) équations linéaires à \(3\) inconnues :
- \(R_4.I + (r_0 + R_3 + R_4).I_0 + (R_3 + R_4).I_1 = 0 \quad(1)\)
- \((R_1 + R_4).I + (R_3 + R_4).I_0 + (R_1 + R_2 + R_3 + R_4).I_1 = 0\quad (2)\)
\((r_i + R_1 + R_4).I - R_4.I_0 - (R_1 + R_4).I_1 = E \quad(3)\)
Qui, compte tenu des valeurs de l'énoncé, s'écrit :
-\(400.I + 900.I_0 + 800.I_1 = 0 \quad(1)\)
-\(700.I + 800.I_0 +1400.I_1 = 0 \quad(2)\)
\(750.I - 400.I_0 - 700.I_1 = 20\quad (3)\)
qui peut être simplifié en :
-\(4.I + 9.I_0 + 8.I_1 = 0 \quad(1)\)
-\(7.I + 8.I_0 + 14.I_1 = 0 \quad(2)\)
\(75.I - 40.I_0 - 70.I_1 = 2 \quad(3)\)
Pour résoudre par substitution, on exprime \(I_1\) en fonction de \(I_0\) et\( I\) en utilisant (1) ou (2) ; on reporte cette expression dans les deux autres équations ; on élimine ensuite soit \(I_0\), soit \(I\) entre les deux équations qui restent, ce qui donne l'inconnue restante.
Par la méthode de Kramer :
\(\displaystyle{I_0=\frac{\left|\begin{array}{ccc}-4&0&8\\-7&0&14\\75&2&-70\end{array}\right|}{\left|\begin{array}{ccc}-4&9&8\\-7&8&14\\75&-40&-70\end{array}\right|}=0}\);
ce qui était prévisible, car le pont est équilibré : \(R_1R_3=R_2R_4\)
\(\displaystyle{I=\frac{\left|\begin{array}{ccc}0&9&8\\0&8&14\\2&-40&-70\end{array}\right|}{\left|\begin{array}{ccc}-4&9&8\\-7&8&14\\75&-40&-70\end{array}\right|}=0,05\textrm{ A}}\)
\(I = 50 \textrm{ mA}\)