Pont de Wheatstone (2)
Partie
Question
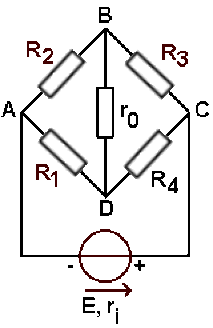
Déterminer les potentiels aux points \(B \textrm{ et }D\).
Application numérique :
\(R_1 = R_2 = 300\;\Omega ; R_3 = R_4 = 400\;\Omega\) ;
\(E = 20 \textrm{ V}\) ;
\(r_i = 50 \;\Omega ; r_0 = 100 \;\Omega\)
Aide simple
Exprimer l'intensité du courant dans chaque branche en fonction de la différence de potentiel entre les noeuds situés aux extrémités, puis appliquer la loi aux nœuds.
Solution simple
\(V_A = V_B = 7,5 \textrm{ V}\)
Solution détaillée
Soient :
I l'intensité débitée par le générateur
\(I_0, I_1, I_2, I_3, I_4\) les intensités dans les branches contenant \(r_0, R_1, R_2, R_3, R_4\)
Calcul des intensités :
\(V_C - V_A = E - r_i.I\) ;
\(\displaystyle{I=\frac{E-(V_C-V_A)}{r_i}}\)
\(\displaystyle{I_1=\frac{V_D-V_A}{R_1}}\)
\(\displaystyle{I_2=\frac{V_B-V_A}{R_2}}\)
\(\displaystyle{I_3=\frac{V_C-V_B}{R_3}}\)
\(\displaystyle{I_4=\frac{V_C-V_D}{R_4}}\)
\(\displaystyle{I_0=\frac{V_B-V_D}{r_0}}\) on suppose\( I_0 > 0\)
Equations aux noeuds :
\(\displaystyle{C : I=I_3+I_4\iff\frac{E}{r_i}-\frac{V_C-V_A}{r_i}=\frac{V_C-V_B}{R_3}+\frac{V_C-V_D}{R_4}}\)
\(\displaystyle{B :I_3=I_0+I_2\iff\frac{V_C-V_B}{R_3}=\frac{V_B-V_D}{r_0}+\frac{V_B-V_A}{R_2}}\)
\(\displaystyle{D :I_1=I_0+I_4\iff\frac{V_D-V_A}{R_1}=\frac{V_B-V_D}{r_0}+\frac{V_C-V_D}{R_4}}\)
\(V_A\) étant le point de potentiel le plus bas, on pose \(V_A = 0\), ce qui donne :
\(\displaystyle{(1)\quad-\frac{V_B}{R_3}+V_C.(\frac{1}{r_i}+\frac{1}{R_3}+\frac{1}{R_4})-\frac{V_D}{R_4}=\frac{E}{r_i}}\)
\(\displaystyle{(2)\quad-\frac{V_C}{R_3}+V_B.(\frac{1}{R_3}+\frac{1}{r_0}+\frac{1}{R_2})-\frac{V_D}{r_0}=0}\)
\(\displaystyle{(3)\quad-\frac{V_B}{r_0}-\frac{V_C}{R_4}+V_D.(\frac{1}{R_1}+\frac{1}{r_0}+\frac{1}{R_4})=0}\)
Après avoir remplacé les résistances et \(E\) par leurs valeurs numériques, et après simplification, il vient :
\(\displaystyle{(1)\quad-V_B+10.V_C-V_D=160}\)
\(\displaystyle{(2)\quad19.V_B-3.V_D-12.V_D=0}\)
\(\displaystyle{(3)\quad-12.V_B-3.V_C+19.V_D=0}\)
Par substitution, on peut à partir de (2) et (3) exprimer \(V_C\) en fonction de\( V_B \textrm{ et }V_D\) ; en reportant cette expression dans les deux autres équations, on obtient deux équations à deux inconnues que l'on résout en éliminant une inconnue, puis l'autre.
Par la méthode de Kramer
\(\displaystyle{V_B=\frac{\left|\begin{array}{ccc}160&10&-1\\0&-3&-12\\0&-3&19\end{array}\right|}{\left|\begin{array}{ccc}-1&10&-1\\19&-3&-12\\-12&-3&19\end{array}\right|}=7,5\textrm{ V}}\)
\(\displaystyle{V_D=\frac{\left|\begin{array}{ccc}-1&10&160\\19&-3&0\\-12&-3&0\end{array}\right|}{\left|\begin{array}{ccc}-1&10&-1\\19&-3&-12\\-12&-3&19\end{array}\right|}=7,5\textrm{ V}}\)
Ce qui était prévisible, car le pont est équilibré : \(R_1R_3=R_2R_4\)