Cinématique dans l'espace temps
Partie
Question
Trajectoire elliptique (**)
Une particule se déplace sur une courbe d'équation :
\(\displaystyle{\overrightarrow r(t)=5\cos\omega t\overrightarrow i+3\sin\omega t\overrightarrow j}\)
Quelle est la nature de cette trajectoire ?
Calculer la norme de la vitesse
Calculer la norme de l'accélération ainsi que sa composante tangentielle.
Aide simple
Utiliser (Cos)(Cos)+ (Sin)(Sin) = 1
Identifier l'équation d'une ellipse
Utiliser la définition de la composante d'un vecteur à l'aide du produit scalaire
Solution détaillée
1) L'équation donne directement\( x = 5 \cos \omega t \textrm{ et }y = 3 \sin \omega t\) et on voit que\( \displaystyle{\frac{x^2}{5^2}+\frac{y^2}{3^2}=1}\)d'où l'on déduit que la trajectoire est une ellipse.
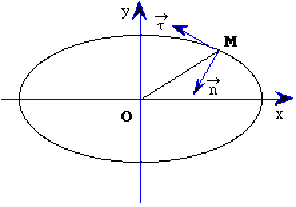
2) Pour la vitesse \(\displaystyle{\overrightarrow v=v_x\overrightarrow i+v_y\overrightarrow j=-5\omega\sin\omega t\overrightarrow i+3\omega\cos\omega t\overrightarrow j}\)
\(\displaystyle{\vert\vert\overrightarrow v\vert\vert=\omega\sqrt{25\sin^2\omega t+9\cos^2\omega t}}\)
3) Accélération et composante tangentielle :
en utilisant \(\displaystyle{\overrightarrow\tau=\frac{\overrightarrow v}{\vert\vert\overrightarrow v\vert\vert}}\), et en dérivant le vecteur vitesse par rapport au temps:
\(\displaystyle{\overrightarrow\gamma=-5\omega^2\cos\omega t\overrightarrow i-3\omega^2\sin\omega t\overrightarrow j}\)
\(\displaystyle{\gamma_t=\overrightarrow\gamma.\overrightarrow\tau=\frac{16\omega\sin\omega t\cos\omega t}{\sqrt{25\sin^2\omega t+9\cos^2\omega t}}}\)
On pourrait ensuite calculer \(\displaystyle{\gamma_n}\) en utilisant le théorème de Pythagore dans le triangle rectangle formé par \(\gamma,\gamma_n,\gamma_t\)
\(\displaystyle{\gamma_n=\sqrt{\gamma^2-\gamma_t^2}}\)