Synthèse

1) Schéma correspondant aux consignes de l'énoncé avec\( \displaystyle{\lambda\in[0,\frac{+\pi}{2}]}\)

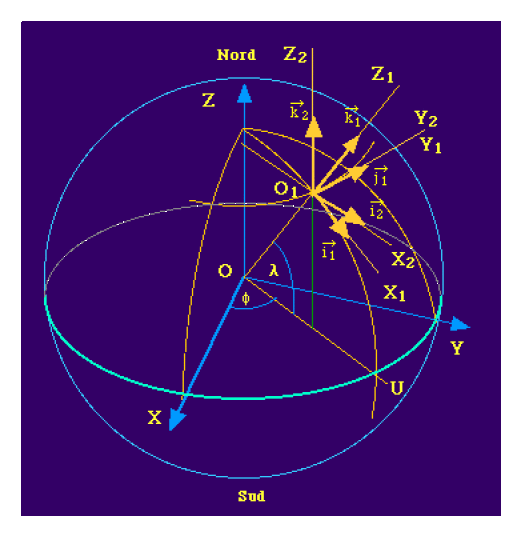
Le plan du méridien passant par \(O_1\) contient les vecteurs représentés sur le schéma ci-dessous. La direction "Vers l'Est" est représentée par le vecteur\( \overrightarrow j_1\) tangent au parallèle passant par \(O_1\).

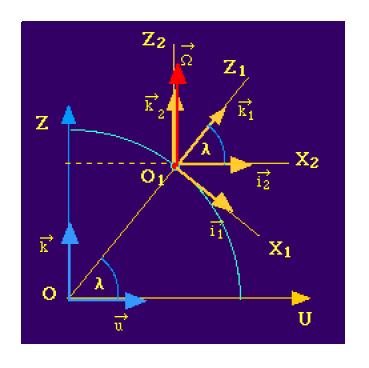
2) La Terre étant supposée faire, dans \(\mathcal R\) , un tour en 24 heures, on a \(\displaystyle{\overrightarrow\Omega=\omega\overrightarrow k}\) avec

\(\displaystyle{\omega=\frac{2\pi}{24.3600}=7,27\;10^{-5}\textrm{ rad/s}}\)

Dans \(\displaystyle{\mathcal R_1(O_1,\overrightarrow i_1,\overrightarrow j_1,\overrightarrow k_1)}\) : il suffit d'exprimer \(\overrightarrow k\) dans cette base. Comme on le voit dans le schéma ci-dessus, si on se place dans le plan (\(O_1, X_1, Z_1\)) confondu avec le plan ( \(OU, OZ\)) où se trouve \(\overrightarrow k\) ,

on a :

\(\displaystyle{\overrightarrow k=-\cos\lambda\overrightarrow i_1+\sin\lambda\overrightarrow k_1\textrm{ d'où }\overrightarrow\Omega_1=-\omega\cos\lambda\overrightarrow i_1+\omega\sin\lambda\overrightarrow k_1}\)

Les vecteurs vitesses de rotation sont indépendants du référentiel et \(\displaystyle{\overrightarrow\Omega=\overrightarrow\Omega_1}\) . Le vecteur\( \overrightarrow V_1\) , vitesse de \(O_1\) par rapport à \(\mathcal R\) s'obtient par définition du vecteur vitesse de rotation \(\displaystyle{\overrightarrow\Omega :\overrightarrow V_1=\overrightarrow\Omega_1\wedge\overrightarrow{OO_1}}\) . En décomposant le produit vectoriel dans la base \((\overrightarrow i_1,\overrightarrow j_1,\overrightarrow k_1)\) :

\(\displaystyle{\begin{array}{cccccc}\overrightarrow V_1&=&(-\omega\cos\lambda\overrightarrow i_1+\omega\sin\lambda\overrightarrow k_1)\wedge R\overrightarrow k_1\\\overrightarrow V_1&=&-\omega R\cos\lambda(\overrightarrow i_1\wedge\overrightarrow k_1)=\omega R\cos\lambda\overrightarrow j_1\end{array}}\)

L'accélération se calcule à partir de la dérivée temporelle de la vitesse :

\(\displaystyle{\overrightarrow\gamma=\frac{\textrm d\overrightarrow v}{\textrm{dt}}=-R\omega^2\cos\lambda(\cos\omega t\overrightarrow i+\sin\omega t\overrightarrow j)}\)

Comme :\( \displaystyle{\overrightarrow u=\cos\omega t\overrightarrow i+\sin\omega t\overrightarrow j\textrm{ ,on a aussi : }\overrightarrow\gamma=-R\omega^2\cos\lambda\overrightarrow u}\).

Ce résultat est évident puisque\( O_1\) est animé d'un mouvement circulaire uniforme de rayon \(R\cos\lambda\) autour de l'axe \(OZ\) dont l'accélération centripète est donnée par la relation

\(\displaystyle{\overrightarrow\gamma=\frac{v^2}{r}\overrightarrow n}\)

qui donne bien le même résultat.

Au cours d'une rotation d'une journée (supposée uniforme et de direction constante), le vecteur\( \overrightarrow\Omega\) est constant; le point \(O_1\) étant immobile à la surface de la Terre, la latitude est constante, toutes les autres grandeurs sont modifiées.

3) \(\mathcal R_1\textrm{ et }\mathcal R_2\) étant liés à la Terre sont entrainés dans la même rotation \(\overrightarrow\Omega\)

On a donc simplement\( \displaystyle{\overrightarrow\Omega_1=\overrightarrow\Omega_2=\overrightarrow\Omega=\omega\overrightarrow k}\) . Dans : \(\mathcal R_1\) :

\(\displaystyle{\overrightarrow k=-\cos\lambda\overrightarrow i_1+\sin\lambda\overrightarrow k_1\textrm{ et }\overrightarrow\Omega_1=-\omega\cos\lambda\overrightarrow i_1+\omega\sin\lambda\overrightarrow k_1}\)

Dans \(\mathcal R_2\) :

\(\displaystyle{\overrightarrow k_2=\overrightarrow k\textrm{ et }\overrightarrow\Omega_2=\omega\overrightarrow k_2}\)