Problèmes de Synthèse
Partie
Question
Mouvements dans un champ newtonien (Partie B: Relation Energie - Conique ) (**)
Les données et résultats de la partie \(A\) du Problème 03 s'appliquent à la partie \(B\). On se propose d'étudier la relation entre l'énergie du satellite et le type d'orbite conique.On prend dans ce qui suit \(\displaystyle{\beta_0=\frac{\pi}{2}}\). On note \(v^*\) la vitesse initiale donnant lieu à une trajectoire circulaire.
Etude de l'orbite circulaire:
Quelle est la valeur de la norme de la vitesse pour obtenir une trajectoire circulaire .
Exprimer alors l'énergie mécanique\( E^*\) en fonction de m et \(v^*\).
Etude des autres orbites
On conserve les conditions initiales :
\(\displaystyle{t=0,\rho=\rho_0,\Phi=0,\beta_0=\frac{\pi}{2}}\) , mais on change la norme de la vitesse initiale qui prend la valeur :\(\displaystyle{v_0=\alpha v^*}\) .
L'énergie mécanique pour la trajectoire circulaire se note alors \(E^*\).
Exprimer l'énergie totale \(E\) en fonction de \(E^*\), de \(\alpha\) et des données du problème.
Tracer la loi de variation de l'énergie\( \displaystyle{\frac{E}{\vert E^*\vert}=f(\alpha)}\)
Quelles valeurs de \(\alpha\) maintiennent la liaison entre le centre attractif et le satellite ?
Pour quelle valeur de \(\alpha\), obtient-on une trajectoire parabolique ?
Quelles valeurs de \(\alpha\) libèrent la particule du champ d'attraction ?
Aide simple
Utiliser les coordonnées intrinsèques Le cercle est une courbe à rayon de courbure constant ...
Faites un schéma avec les divers vecteurs de base intervenant.
Passer par l'expression donnant l'excentricité en fonction de l'énergie pour raisonner
\(\displaystyle{\textrm e^2-1=\frac{2\sigma_0^2E}{mK^2}=\frac{2mC^2E}{K^2}}\)
L'énergie de la trajectoire circulaire sert d'unité de fonctionnement pour raisonner\( (\textrm e = 0)\) et l'énergie de la parabole sert de borne entre trajectoires ouvertes et fermées\( (\textrm e = 1)\)
Solution détaillée
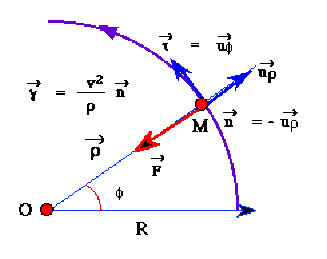
Lorsque le mouvement est à accélération centrale, avec une composante tangentielle nulle, la trajectoire circulaire est forcément uniforme\( (\displaystyle{\frac{\textrm dv}{\displaystyle dt}=0})\) . L'accélération est telle que
\(\displaystyle{\overrightarrow\gamma=\frac{v^{*2}}{\rho_0}\overrightarrow n\textrm{ où }\overrightarrow n=-\overrightarrow u_\rho}\)
D'autre part,
\(\displaystyle{\overrightarrow\gamma=\frac{\overrightarrow F}{m}=-\frac{k}{m\rho^2}\overrightarrow u_\rho}\)
ce qui donne \(\displaystyle{k=m\rho_0v^{*2}}\) et
\(E^*\) énergie mécanique pour l'orbite circulaire égale à :
\(\displaystyle{E^*=\frac{1}{2}mv^{*2}-\frac{k}{\rho_0}}\)
et en remplaçant k par sa valeur : L'énergie mécanique pour l'orbite circulaire est négative et égale en valeur absolue à l'énergie cinétique et à la moitié de l'énergie potentielle.
Si on pose \(\displaystyle{v_0=\alpha v^*}\) et si on calcule l'énergie mécanique pour une orbite quelconque, on obtient :
\(\displaystyle{E=\frac{1}{2}m\alpha^2v^{*2}-\frac{k}{\rho}}\)
or, l'énergie étant constante au cours du mouvement est égale à son énergie initiale et comme la masse m reste placée à l'instant initial au même endroit, l'énergie potentielle est la même que pour l'orbite circulaire , soit \(\displaystyle{\frac{k}{\rho_0}}\); il suffit de remplacer k par sa valeur et on obtient :
\(\displaystyle{E=\frac{1}{2}m\alpha^2v^{*2}-mv^{*2}=(2-\alpha^2)E^*}\)
soit en unités\( \displaystyle{\vert E^*\vert}\) :
\(\displaystyle{\frac{E}{\vert E^*\vert}=(\alpha^2-2)}\)

Pour les différentes valeurs de \(\alpha\), on trouve les diverses coniques :
si \(\alpha=1\) : on a le cercle
si \(1<\alpha<\sqrt2\), on a l'ellipse
si\( \alpha=\sqrt2\) , on a la parabole
si \(\alpha>\sqrt2\) , on a l'hyperbole
Les trajectoires qui s'éloignent à l'infini sont celles dont l'énergie mécanique est positive (la particule n'est pas liée) ; cela correspond aux valeurs de \(\alpha\ge q\sqrt2\) .