Problèmes de Synthèse
Partie
Question
Le champ d'accélération d'entraînement de la Terre
On considère un référentiel orthonormé direct \(\displaystyle{\mathcal G :(O,\overrightarrow i,\overrightarrow j,\overrightarrow k)}\) dont le centre se confond avec le centre de la Terre, supposée sphérique de rayon \(R\), et dont les axes sont dirigés vers des étoiles fixes. L'axe \(O_z\) est confondu avec l'axe des pôles (axe de rotation) et son sens est \(\textrm{Sud} \to \textrm{Nord}\). Soit \(M\) un point de la surface terrestre. Le plan \((OZ, OM)\) coupe le plan \(XOY\) selon l'axe \(O_u\). Le référentiel \(\mathcal R :(O,\overrightarrow u_\rho,\overrightarrow u_\Phi,\overrightarrow k)\)est lié à la Terre et tourne avec elle.
Quelle est l'expression vectorielle de l'accélération d'entraînement \(\overrightarrow\gamma_e(M)\) à laquelle est soumis le point \(M\) au cours de la rotation terrestre.
Quelle est l' expression de \(\overrightarrow\gamma_e(M)\) dans la base \((\overrightarrow u_\rho,\overrightarrow u_\Phi,\overrightarrow k)\) ?
En quels points du globe est-elle maximale ?
En quels points du globe est-elle nulle ?
L'accélération \(\overrightarrow\gamma_e(M)\) est-elle un champ de vecteurs ? Si non, pourquoi.
Si oui, quelle est la symétrie de ce champ ?
Existe-t-il des plans dans lesquels sa norme est constante ?
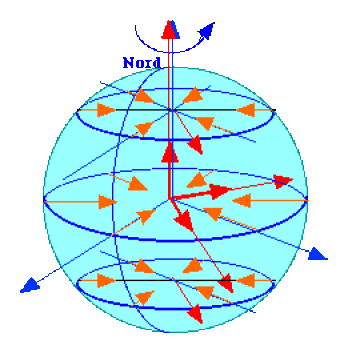
Dessiner le champ de vecteurs pour des points qui appartiennent à différents parallèles en visualisant les variations des vecteurs.
Calculer le potentiel scalaire \(T(\rho)\) dont dérive ce champ de vecteurs.sachant que \(T(0) = 0\).
Que représente ce potentiel scalaire en tant que grandeur physique ?
Aide simple
exprimer la forme la plus générale de l'accélération d'entrainement d'un référentiel \(R\) animé d'un mouvement de rotation par rapport à un autre référentiel \(G\)
exprimer ensuite cette accélération dans le cas de l'énoncé : pas de translation + rotation uniforme
Un champ cylindrique est porté par le vecteur polaire et sa norme ne dépend que de la distance à l'axe.
Se placer en coordonnées cylindriques pour calculer le gradient.
La dérivée partielle par rapport à une variable se confond avec la dérivée totale lorsqu'il n'y a qu'une variable.
Solution détaillée
1)
La forme la plus générale de\( \overrightarrow\gamma_e(M)\) s'écrit :
\(\displaystyle{\overrightarrow\gamma(O)+\overrightarrow\Omega\wedge(\Omega\wedge\overrightarrow{OM})+\frac{\textrm d\overrightarrow\Omega}{\textrm{dt}}\wedge\overrightarrow{OM}}\)
Dans le cas particulier de la rotation uniforme \(\displaystyle{(\frac{\textrm d\overrightarrow\Omega}{\textrm{dt}}=\overrightarrow0)}\) autour d'un axe (sans mouvement de translation :
\(\displaystyle{\overrightarrow\gamma(O)=\overrightarrow0 :\overrightarrow\gamma_e(M)=\overrightarrow\Omega\wedge(\overrightarrow\Omega\wedge\overrightarrow{OM})}\)
Dans la base\( (\displaystyle{\overrightarrow u_\rho,\overrightarrow u_\Phi,\overrightarrow k})\) :
\(\displaystyle{\overrightarrow{OM}=\rho\overrightarrow u_\rho+z\overrightarrow k\textrm{ et }\overrightarrow\Omega=\Omega\overrightarrow k}\)
d'où
\(\displaystyle{\overrightarrow\Omega\wedge\overrightarrow{OM}=\Omega_\rho\overrightarrow u_\rho\wedge\overrightarrow k=\Omega R\sin\Phi\overrightarrow u_\Phi}\)
où \(\theta\) est la colatitude \((\overrightarrow k,\overrightarrow u_\rho)\) , coordonnée utilisée en coordonnées sphériques.
\(\displaystyle{\overrightarrow\gamma_e(M)=-\Omega^2R\sin\Phi\overrightarrow u_\rho}\)
A l'Equateur\( \displaystyle{\overrightarrow\gamma_e(M)=-\Omega^2R}\) est maximum ; aux pôles\( \displaystyle{\overrightarrow\gamma_e(M)=\overrightarrow0}\).
2) Pour un point
\(\displaystyle{M\in\textrm{ Surface de la Terre : M}\to\overrightarrow\gamma_e(M)=-\Omega^2R\sin\Phi\overrightarrow u_\rho=-\Omega^2\rho\overrightarrow u_\rho}\)
C'est la définition d'un champ de vecteurs de la forme \(\displaystyle{f(\rho)\overrightarrow u_\rho}\) . La symétrie du champ est axiale : l'axe des pôles étant l'axe de symétrie. Le champ à la surface de la Terre provenant de l'accélération d'entraînement est un champ axial (selon\( \overrightarrow u_\rho\) ) et il ne dépend que de la distance à l'axe, donc cylindrique.
3) Le potentiel scalaire \(T(\rho)\) est tel que :
\(\displaystyle{\overrightarrow{\gamma_e}(M)=-\Omega^2\rho\overrightarrow u_\rho}\)
doit être son gradient. On doit donc avoir :
\(\displaystyle{-\Omega^2\rho\overrightarrow u_\rho=-\overrightarrow{\textrm{gradM}}T=-\frac{\delta T}{\delta\rho}\overrightarrow u_\rho=-\frac{\textrm dT}{\textrm d\rho}\overrightarrow u_\rho}\)
car l'accélération ne dépend que de \(\rho\). L'expression du potentiel scalaire est telle que :
T(r) a la dimension du carré d'une vitesse et correspond à une énergie cinétique de rotation pour une masse unité placée en M.