Problèmes de Synthèse
Partie
Question
Principe d'inertie pour systèmes pseudo-isolés et isolés - B (Référentiel du laboratoire) (**)
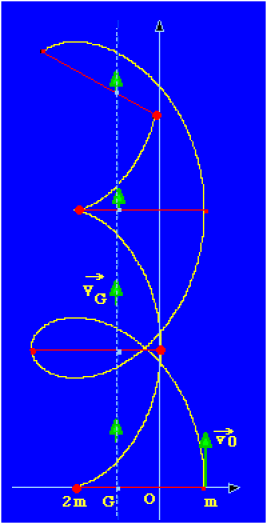
4) Dans le référentiel du laboratoire, quel est le mouvement de chaque palet ? Représentez sur un même graphique l'allure des trajectoires de \(G, \textrm{ de }M_1 \textrm{ et de }M_2\).
5) Soit \(S_{12}\) un système de deux masses \(m_1 \textrm{ et }m_2\) en interaction gravitationnelle, animées par rapport à un galiléen \(\mathcal G\) des vitesses\( \overrightarrow v_1\textrm{ et }\overrightarrow v_2\). Ce système n'est soumis à aucune autre interaction. A un instant pris pour initial,
\(m_1 \textrm{ est en }M_1\textrm{ tel que }\overrightarrow{OM}_1=2\overrightarrow i,a>0\)
\(m_2\textrm{ est en }M_2\textrm{ tel que }\overrightarrow{ OM}_2=-a\overrightarrow i\)
\(\overrightarrow{v_{t_0}}(M_1)=\overrightarrow v_1=v_0\overrightarrow j,\overrightarrow v_{t_0}(M_2)=\overrightarrow v_2=0\)
Comparez les systèmes \(S_{12} \textrm{ et }(S)\).
Calculer l'énergie cinétique et l'énergie potentielle du système équivalent \(\sum\) défini par sa masse "réduite"
\(\displaystyle{\mu=\frac{m_1m_2}{m_1+m_2}}\)
Exprimer l'énergie mécanique de \(\sum\) .
Aide simple
On est ramené au problème à deux corps en interaction centrale.
Les grandeurs cinétiques se définissent comme pour un seul corps mais avec la masse réduite du système au lieu de la masse de la particule.
Solution détaillée
4) Dans le référentiel du laboratoire, la vitesse de chaque palet est la somme vectorielle de sa vitesse dans \(G\) et de la vitesse du centre d'inertie par rapport au laboratoire :
\(\displaystyle{\overrightarrow{v(P_1)}_{/\textrm{labo}}=\overrightarrow{v(P_1)}/G+\overrightarrow v_{G/\textrm{labo}}=2a\omega\overrightarrow u_\theta+\frac{v_0}{3}\overrightarrow j}\)
\(\displaystyle{\overrightarrow{v(P_2)}_{/{\textrm{labo}}}=\overrightarrow{v(P_2)}/G+\overrightarrow{v}_{G/\textrm{labo}}=-a\omega\overrightarrow u_\theta+\frac{v_0}{3}\overrightarrow j}\)
La composition d'une translation uniforme et d'une rotation unforme donne une cycloïde. On obtient donc deux cycloïdes emboitées.
L'expression mathématique complète des trajectoires n'était pas demandée.
5) \(S_{12}\) a en commun avec \((S)\) d'être un système comportant des forces centrales égales et opposées : ce sont d'autre part des systèmes isolés ou pseudo-isolés. Dans les deux cas, les solutions s'obtiennent par l'application du principe d'inertie
\(\displaystyle{\frac{\textrm d}{\textrm{dt}}\overrightarrow P=\overrightarrow0}\)
car la résultante des forces est nulle
\(\displaystyle{\frac{\textrm d}{\textrm{dt}}\overrightarrow\sigma=\overrightarrow0}\)
car le moment résultant est nul. L'énergie cinétique de \(S_{12}\) s'obtient à partir de \(\displaystyle{T=\frac{1}{2}\mu V^2}\) , où \(\mu\) est la masse réduite du système équivalent qui est ici égale à \(2\textrm m/3\) et où \(\textrm V\) est la vitesse relative de la particule 2 par rapport à la particule 1. Ici,
\(\displaystyle{\overrightarrow V=-a\omega\overrightarrow u_\theta-2a\omega\overrightarrow u_\theta=-3a\omega\overrightarrow u_\theta}\)
ce qui donne
\(\displaystyle{T=\frac{1}{2}\frac{2\textrm m}{3}9a^2\omega^2=3\textrm ma^2\omega^2}\)
Remarques :
a) On retrouve bien une forme connue de l'énergie cinétique en \(I\) où \(I\) est une grandeur positive qui dépend de la masse et de la distance au centre d'inertie (Ici, \(I = \textrm ma^2 + 2\textrm ma^2\)). L'énergie potentielle ne dépend que des positions relatives des masses donc ici, de la distance \(M_1 M_2\)
\(\displaystyle{U=-G\frac{m\cdot2\textrm m}{3a}=-\frac{2}{3}G\frac{\textrm m^2}{a}}\)
Au total, l'énergie mécanique :
\(\displaystyle{E=T+U=3\textrm ma^2\omega^2-\frac{2}{3}G\frac{\textrm m^2}{a}}\)
b) Il s'agit ici de l'énergie "propre" soit par rapport au référentiel barycentrique. Pour déterminer l'énergie par rapport à un autre galiléen il faudrait ajouter l'énergie cinétique de translation
\(\displaystyle{\frac{1}{2}M\overrightarrow{v^2}_{G/\textrm{labo}}}\)
où \(M\) serait la masse totale concentrée au centre d'inertie.