Synthèse

Pour les questions 1, 2 et 4, on se place dans le référentiel du laboratoire. La question 3 se place dans le référentiel barycentrique.

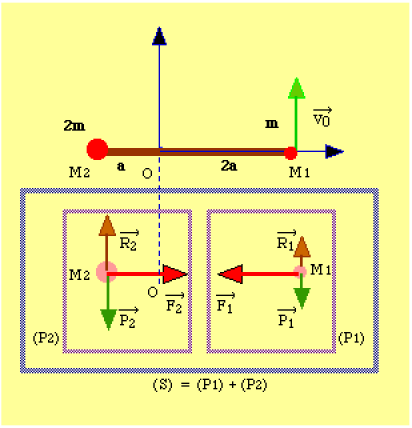
1. (S) est constitué des deux palets et de la tige de masse négligeable. Chaque palet est soumis à son poids, à la réaction du plan horizontal et une réaction due à la présence de la tige qui rigidifie l'ensemble. Pour chaque palet, le poids équilibre la réaction par absence de frottement et il ne reste que la réaction de la tige dirigée vers l'intérieur de celle-ci. L'ensemble est donc soumis en définitive à une somme des forces nulle : (S) est pseudo-isolé. Son centre d'inertie \(G\) est tel que

   \(\displaystyle{\overrightarrow{OG}=\frac{1}{M}\sum_{i=1}^Nm_i\overrightarrow{OM}_i}\)

   [On peut aussi écrire : \(\displaystyle{\sum_{i=1}^{N}m_i\overrightarrow{GA}_i=\overrightarrow0\Rightarrow m\overrightarrow{GP}_1+2m\overrightarrow{GP}_2=\overrightarrow0\;\overrightarrow{GP}_1=-2\overrightarrow{GP}_2}\)]

   On trouve, avec les valeurs de l'énoncé,\( \overrightarrow{OG}=\overrightarrow0\Rightarrow G\)  est en \(O\).

   Le centre d'inertie d'un système pseudo-isolé a un mouvement rectiligne uniforme. Sa vitesse s'obtient en appliquant l'additivité de la quantité de mouvement; étant constante, on peut la calculer à l'instant initial pour lequel \(\displaystyle{\overrightarrow p_2=\overrightarrow0}\):

   \(\displaystyle{\begin{array}{cccccc}\overrightarrow P&=&(m+2m)\overrightarrow v_G\\\overrightarrow P&=&\overrightarrow p_1+\overrightarrow p_2=M.v_0\overrightarrow j+\overrightarrow0\end{array}}\)

   d'où \(\displaystyle{\overrightarrow v_G=\frac{v_0}{3}\overrightarrow j}\)

2. Calcul du moment cinétique : par rapport à \(O\) (ou par rapport à \(G\)). Le moment cinétique de \((S)\) est la somme des moments cinétiques de \((P_1)\) et \((P_2)\) :

   \(\displaystyle{\overrightarrow{\sigma/G}=\overrightarrow{\sigma_1/G}+\overrightarrow{\sigma_2/G}}\)

   A un instant \(t\) quelconque, le système étant pseudo-isolé, a son moment résultant nul donc :

   \(\displaystyle{\frac{\textrm d}{\textrm dt}\overrightarrow\sigma=\overrightarrow0\Rightarrow\overrightarrow\sigma=\textrm{Cste}}\)

   On peut le déterminer par sa valeur à l'instant initial :

   \(\displaystyle{\overrightarrow{\sigma_1/G}=\overrightarrow{GM}_1\wedge mv_0\overrightarrow j=2a\overrightarrow i\wedge mv_0\overrightarrow j=2amv_0\overrightarrow k}\)

   Le moment cinétique n'est pas nul, ce qui implique un mouvement de rotation du système dont le vecteur de base est \(\overrightarrow k\) , attaché à \(G\).

   Tout point de ce système décrit par rapport à l'axe de rotation \(\overrightarrow k\) , une circonférence de rayon égal à la distance à l'axe : par suite, la norme de la vitesse à un instant t quelconque s'écrit, avec \(\omega\) quelconque :

   Pour \((P_1)\) :\(\overrightarrow v_1=2a\omega\overrightarrow u_\theta\textrm{ avec }\overrightarrow u_\theta\) le vecteur tangent en \(M_1\) à la circonférence

   Pour \((P_2)\) :\( \displaystyle{\overrightarrow v_2=a\omega\overrightarrow u_{\theta_2}=-a\omega\overrightarrow u_{\theta_1}}\) car, au même instant \(\displaystyle{\overrightarrow u_{\theta_2}=-\overrightarrow u{\theta_1}}\).

   L'expression à un instant t quelconque donne :

   \(\displaystyle{\overrightarrow{\sigma/G}=\overrightarrow{\sigma_1/G}+\overrightarrow{\sigma_1/G}}\)

   \(\displaystyle{\begin{array}{cccccc}\overrightarrow{\sigma/G}&=&\overrightarrow{GM}_1\wedge\overrightarrow p_1+\overrightarrow{GM}_2\wedge\overrightarrow p_2\\&=&2a\overrightarrow u_\rho\wedge m2a\omega\overrightarrow u_\theta+(-a\overrightarrow u_\rho)\wedge(-2ma\omega\overrightarrow u_\theta)\\\overrightarrow{\sigma/G}&=&2am3a\omega\overrightarrow k\end{array}}\)

   On a montré plus haut que le moment cinétique était constant et avait pour valeur :

   \(\displaystyle{\overrightarrow{\sigma/G}=2amv_0\overrightarrow k}\)

   Ceci permet de montrer que le mouvement circulaire est uniforme car \(\omega\) est constant et tel que : \(3a\omega = v_0\)

   On retrouve le principe d'inertie pour un solide : si le solide est isolé, et possède un moment cinétique initial (donc un élan de rotation), chaque point du solide effectue un mouvement circulaire uniforme. Chaque point possède, évidemment, la même vitesse angulaire mais la vitesse linéaire dépend de la distance à l'axe de rotation.

3. On se place dans le référentiel barycentrique nommé \(G\) et qui est ici galiléen. Le mouvement de translation rectiligne uniforme du centre d'inertie est alors annulé. On a donc seulement une rotation uniforme du système autour de \(G\).

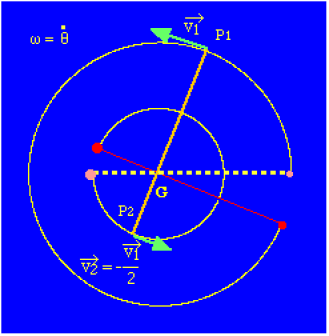
Dans ce cas, la quantité de mouvement totale est nulle :

\(\displaystyle{\overrightarrow P=\overrightarrow0\Rightarrow\overrightarrow p_1=-\overrightarrow p_2\Rightarrow v_1=-2\overrightarrow v_2}\)