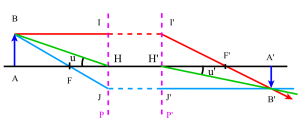
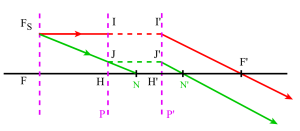
Equation de conjugaison
Partie
Question
Lorsque les positions d'un objet et de son image sont connues, l'équation de conjugaison avec origine aux foyers permet d'aboutir au module, dans l'air, de la distance focale image \(f '\) d'un système centré.
Définir une méthode expérimentale qui permettrait d'établir le signe de la distance focale image d'un système quelconque.
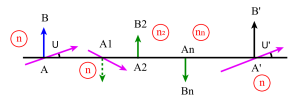
Appliquer le raisonnement à l'étude du signe de la vergence du système centré donné ci-dessous, c'est-à-dire pour un observateur qui voit l'image \(A_2B_2\) de \(A_1B_1\).
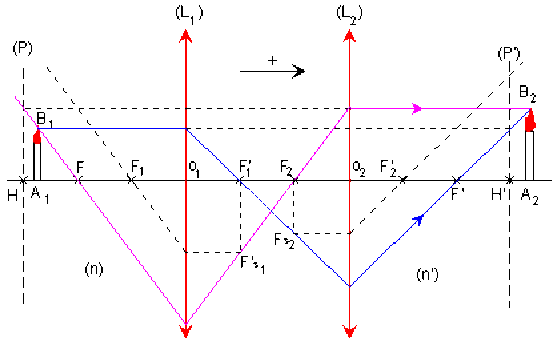
Pensez au grandissement.
Aide simple
Le signe de la vergence d'un système, \(V = n'/f '\) est identique à celui de sa distance focale image. Les expressions du grandissement algébrique \(\frac{\overline{A_{2}B_{2}}}{\overline{A_{1}B_{1}}}=-\frac {f}{\overline{FA_{1}}}=-\frac{\overline{F'A_{2}}}{f'}=\frac {n}{n'}\cdot \frac{\overline{H'A_{2}}}{\overline{HA_{1}}}\) et du rapport \(\frac f{f'}=-\frac n{n'}\), valables pour tout système centré dioptrique donnent au moins deux pistes pour accéder au signe de la distance focale image : l'une à partir de la position de l'objet, l'autre à partir de la position de l'image.
Rappel de cours
Relation de Lagrange-Helmholtz entre l'objet \(AB\) et son image \(A'B'\) :
\(n\overline{AB}u=n'\overline{A'B'}u'\)
Les plans principaux sont deux plans de front conjugués : le plan principal objet et le plan principal image pour lesquels le grandissement linéaire (ou transversal) est égal à +1.
Relation entre les distances focales objet \(f\) et image \(f'\) :
\(\frac{f'}{f}=-\frac{n'}n\)
La vergence d'un système centré sera défini par :
\(V=\frac{n'}{f'}=-\frac nf\)
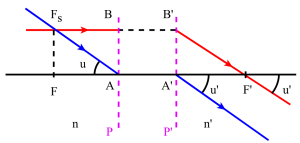
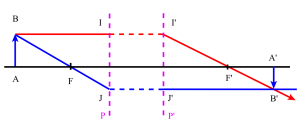
Construction de l'image d'un objet plan. On utilisera 2 rayons particuliers :
l'un issu de \(B\) et parallèle à l'axe optique : il émerge après le plan principal image en passant par le foyer image \(F'\)
l'autre issu de \(B\) et passant par le foyer objet \(F\) : il émerge après le plan principal image, parallèle à l'axe optique
Construction de l'émergent correspondant à un incident quelconque. On utilisera les mêmes rayons particuliers que ceux qui ont servi à construire l'image d'un objet \(AB\).
Formules de conjugaison :
Origine aux points principaux :
si : \(\overline{HA}=p\) et \(\overline{H'A'}=p'\) : \(\frac fp+\frac{f'}{p'}=1\) \(\frac{n'}{p'}-\frac np=\frac{n'}{f'}=C\) avec C vergence du système.
Origine aux foyers: formules de Newton :
si \(\overline{FA}=x\) et \(\overline{F'A'}=x'\) : \(\begin{array}{l}x\cdot x'=f\cdot f'\\\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac fx=-\frac{x'}{f'}\end{array}\)
grandissement angulaire : \(G=\frac{u'}u=\frac n{n'}\frac{\overline{AB}}{\overline{A'B'}}\)
produit du grandissement linéaire par le grandissement angulaire : \(\gamma\cdot G=\frac n{n'}\)
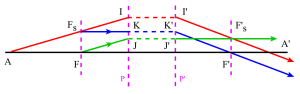
Les plans antiprincipaux sont deux plans conjugués entre lesquels le grandissement est égal à -1. Ce sont les symétriques des plans principaux par rapport aux foyers correspondants (de même pour les plans antiprincipaux).
Les points nodaux \(N\) et \(N'\) sont deux points conjugués, situés sur l'axe, et tels qu'à tout rayon incident passant par le point nodal objet, corresponde un rayon émergent passant par le point nodal image et parallèle au rayon incident.
Les éléments cardinaux d'un système centré comportent: les foyers, les points principaux et antiprincipaux, les points nodaux et antinodaux.
Lorsque pour un système centré donné on connaît deux couples d'éléments cardinaux ou un couple et une distance focale alors le système centré est parfaitement défini.
Solution détaillée
Dans l'air \(n = 1 = n'\) et \(f/f ' = -1\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{-f}{\overline{FA_1}}=\frac{f'}{\overline{FA_1}}\) donne \(f'=\gamma\cdot\overline{FA_1}\)
Il est toujours possible de trouver un objet très éloigné de sorte que \(\overline{FA_1}\) soit négatif.
Si l'image de cet objet, vue à travers le système, est dans le même sens que l'objet \(g > 0\), le signe de \(f '\) est négatif \((\gamma > 0)\times(\overline{FA_1} < 0)\)(sinon il est positif).
Pour le système représenté, le plus simple est de déterminer le signe du segment \(\overline{FA_1}\) en cherchant la position du foyer objet \(F\) à l'aide d'un objet très éloigné et en transformant \(F\) en foyer image par retournement du système. Ce système centré est divergent car sa distance focale est négative \(\overline{FA_1} < 0\).
\(f'=\overline{H'F'} < 0=(\gamma)\cdot\overline{FA_1}=( > 0)\cdot( < 0)=( < 0)\)
La seconde méthode est de partir d'une image de position connue par rapport au foyer image.
Ici \(\overline{F'A_2} > 0\quad\gamma=-\overline{F'A_2}/f'\)Þ\(f'=-\overline{F'A_2}/\gamma\)Þ\(f'=-(\overline{F'A_2} > 0)/(\gamma > 0) < 0\)
Si l'image fournie par le système est réelle, il suffit d'observer le sens de cette image sur un écran. C'est le cas représenté ici. Si l'image est virtuelle, une observation à l'œil nu est possible et le signe du grandissement immédiat (l'image ne peut être que droite ou renversée).