Association de deux lentilles minces
Partie
Question
On dispose de trois lentilles dont les vergences dans l'air sont +5D, +5D, - 5D.
Calculer les distances \(S_1S_2=e\) des combinaisons de deux de ces lentilles qui formeraient dans l'air un système centré convergent d'un mètre de distance focale.
Vérifier géométriquement la vraisemblance des résultats trouvés.
Utiliser la distance focale image d'un doublet
Aide simple
Si \(\Delta=\overline{F'_1F_2}\) est la distance entre les foyers d'un doublet \(L_1L_2\), la distance focale image de ce doublet est : \(f'=-\frac{f'_1\cdot f'_2}\Delta\) avec \(f'_1=\pm f'_2=\pm\frac1{5}=\pm0,2\textrm m\).
Un système centré est convergent si sa distance focale image \(f'\) est positive.
Rappel de cours
Association de deux systèmes centrés
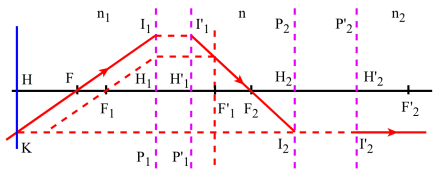
Chacun des deux systèmes sera caractérisé par :
ses foyers objet et image \(F_1\) et \(F'_1\) pour le premier système, \(F_2\) et \(F'_2\) pour le deuxième système.
ses points principaux objet et image: \(H_1\) et \(H'_1\) pour le premier, \(H_2\) et \(H'_2\) pour le deuxième
ses distances focales objet et image : \(f_1=\overline{H_1F_1}\) et \(f'_1=\overline{H'_1F'_1}\) pour le premier et \(f_2=\overline{H_2F_2}\) et \(f'_2=\overline{H'_2F'_2}\) pour le deuxième.
Le premier système sépare les milieux d'indice \(n_1\) et \(n\) tandis que le deuxième sépare les milieux d'indice \(n\) et \(n_2\).
L'ensemble des deux systèmes est caractérisé par une distance définie par : \(\Delta=\overline{F'_1F_2}\) que l'on appelle intervalle optique.
Détermination du foyer objet :
Si l'on veut que le rayon émergent du second système soit parallèle à l'axe il faut que l'incident sur le deuxième système passe par le foyer objet \(F_2\). Le foyer objet \(F\) de l'ensemble des deux systèmes sera donc défini comme étant l'image de \(F_2\) à travers le premier système.
Les formules de Newton appliquées au premier système conduisent à : \(\overline{F_1F}\cdot\overline{F'_1F_2}=f_1\cdot f'_1\)
La position du foyer objet de l'ensemble des deux systèmes sera donc défini par : \(\overline{F_1F}=\frac{f_1\cdot f'_1}\Delta\)
Détermination du foyer image :
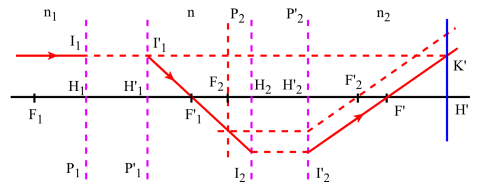
Un rayon parallèle à l'axe du système et incident sur le premier système émergera de celui-ci en passant par le foyer image \(F'_1\). Le foyer image \(F'\) de l'ensemble des deux systèmes ne sera autre que l'image de \(F'_1\) à travers le deuxième système.
En appliquant les formules de Newton on obtient : \(\overline{F_2F'_1}.\overline{F'_2F'}=f_2.f'_2\)
La position du foyer image \(F'\) de l'association des deux systèmes centrés sera donc définie par : \(\overline{F'_2F'}=\frac{f_2\cdot f'_2}\Delta\)
Détermination des plans principaux et des distances focales :
On a vu que le plan principal objet est le lieu des points d'intersection entre un rayon incident et un rayon émergent parallèle à l'axe du système centré. C'est donc le lieu des points \(K\) dont la projection sur l'axe est \(H\) qui constitue le point principal objet.
En appliquant le théorème de Thalès : \(\frac{\overline{FH}}{\overline{FH_1}}=\frac{\overline{HK}}{\overline{H_1I_1}}=\frac{\overline{H_2I_2}}{\overline{H'_1I'_1}}=\frac{\overline{F_2H_2}}{\overline{F_2H'_1}}\) soit : \(\frac{\overline{HF}}{\overline{H_1F_1}+\overline{F_1F}}=\frac f{f_1+\frac{f_1f'_1}{\Delta}}=\frac{\overline{H_2F_2}}{\overline{H'_1F'_1}+\overline{F'_1F_2}}=\frac{f_2}{f'_1+\Delta}\)
La distance focale objet \(f\) est donc définie par : \(f=\overline{HF}=\frac{f_1f_2}\Delta\)
De même on définit le plan principal image comme étant le lieu des points d'intersection entre un rayon incident parallèle à l'axe du système centré et le rayon émergent correspondant. C'est donc le lieu des points \(K'\) dont la projection sur l'axe est \(H'\) qui constitue le point principal image.
On aura de la même façon : \(\frac{\overline{F'H'}}{\overline{F'H'_2}}=\frac{\overline{H'K'}}{\overline{H'_2I'_2}}=\frac{\overline{H'_1I'_1}}{\overline{H_2I_2}}=\frac{\overline{F'_1H'_1}}{\overline{F'_1H'_2}}\) soit : \(\frac{\overline{H'F'}}{\overline{H'_2F'_2}+\overline{F'_2F'}}=\frac{f'}{f'_2-\frac{f_2f'_2}\Delta}=\frac{\overline{H'_1F'_1}}{\overline{H_2F_2}+\overline{F_2F'_1}}=\frac{f'_1}{f_2-\Delta}\)
La distance focale image \(f'\) est donc définie par : \(f'=\overline{H'F'}=\frac{f'_1f'_2}\Delta\)
On remarquera que tout rayon incident passant par \(F_1\) émerge du premier système parallèlement à l'axe et converge après le second système en passant par \(F'_2\). Les points \(F_1\) et \(F'_2\) sont donc conjugués par rapport à l'ensemble du système.
On a d'autre part les relations suivantes : \(\frac{f'_1}{f_1}=-\frac n{n_1}\) et \(\frac{f'_2}{f_2}=-\frac{n_2}n\) on en déduit la relation : \(\frac{f'}f=-\frac{n_2}{n_1}\)
Détermination de la vergence de l'ensemble des deux systèmes :
Les vergences de chacun des systèmes sont données par :
\(C_1=-\frac{n_1}{f_1}=\frac n{f'_1}\)
\(C_2=-\frac n{f_2}=\frac{n_1}{f'_2}\)
tandis que la vergence de l'ensemble des deux systèmes est donnée par : \(C=\frac{n_2}f=-\frac{n_2\Delta}{f'1f'_2}\)
mais \(\Delta=\overline{F'_1F_2}=\overline{F'_1H'_1}+\overline{H'_1H_2}+\overline{H_2F_2}=-f'_1+f_2+\overline{H'_1H_2}\)
ce qui nous permet d'en déduire : \(C=\frac{n_2}{f'_2}-\frac{n_2f_2}{f'_1f'_2}-\frac{n_2}{f'_1f'_2}\overline{H'_1H_2}\)
soit encore la formule de Gullstrand :
\(C=C_1+C_2-\frac{\overline{H'_1H_2}}nC_1C_2\)
Solution détaillée
La distance focale image d'un doublet \(f'=-\frac{f'_1f'_2}{\overline{F'_1F_2}}\) donne les solutions théoriques \(\overline{F'_1F_2}=-\frac{f'_1f'_2}{f'}\) avec \(f ' >0\) :
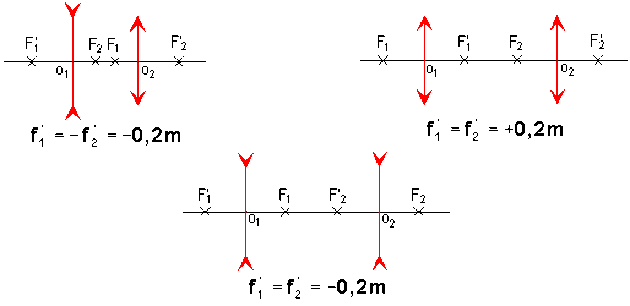
avec 2 lentilles convergentes \(\overline{F'_1F_2}=-\frac{(+0,2\textrm m)\cdot(+0,2\textrm m)}{+1\textrm m}=-0,04\textrm m\)
soit \(\overline{O_1O_2}=\overline{OF'_1}+\overline{F'_1F_2}+\overline{F_2O_2}=0,36\textrm m\)
Le foyer secondaire objet \(F_{2s}\) qui a son image à l'infini donne la direction du rayon émergent. On vérifie schématiquement \(\overline{H'F'}\#+1\textrm m\).
avec 2 lentilles de vergence opposées \(\overline{F'_1F_2}=-\frac{(0,2\textrm m)\cdot(-0,2\textrm m)}{+1\textrm m}=+0,04\textrm m\)
soit \(\overline{O_1O_2}=-\overline{OF'_1}+\overline{F'_1F_2}+\overline{F_2O_2}=-0,2+0,04+0,02=0,04\textrm m\)
On vérifie schématiquement \(\overline{H'F'}\#+1\textrm m\).
avec 2 lentilles divergentes \(\overline{F'_1F_2}=-\frac{(-0,2\textrm m)\cdot(-0,2\textrm m)}{+1\textrm m}=-0,04\textrm m\)
solution impossible puisque \(F'_1F_2\) est toujours positif.
Autre raisonnement :
soit \(\overline{O_1O_2}=-\overline{OF'_1}-\overline{F'_1F_2}-\overline{F_2O_2}=-0,2-0,2-0,04=0,44\textrm m\)
solution impossible puisque \(O_1O_2>0\).