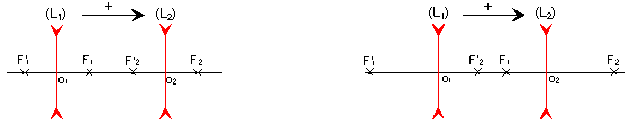Lentilles minces
Partie
Question
Vérifier algébriquement et à l'aide d'un schéma qu'une association de lentilles minces divergentes ne peut pas donner un système convergent.
Qu'est-ce qu'un système convergent ?
Aide simple
Un système est convergent, si sa distance focale image est positive.
La distance focale image d'un système est la mesure algébrique du segment qui sépare le point principal image \(H'\) du foyer image \(F'\) : \(f'=\overline{H'F'}\).
La distance focale image d'un doublet de lentilles \((L_1)\) et \((L_2)\) est donnée par :
(1) \(f'=-\frac{f'_1\cdot f'_2}\Delta\) avec \(\Delta=\overline{F'_1F_2}\)
Aide détaillée
Quel que soient les modules des distances focales et l'écartement de deux lentilles divergentes \((L_1)\), \((L_2)\), les foyers \(F'_1\) et \(F_2\) sont respectivement avant et après les lentilles \(L_1\), \(L_2\).
Rappel de cours
Relation de Lagrange-Helmholtz entre l'objet \(AB\) et son image \(A'B'\) :
\(n\overline{AB}u=n'\overline{A'B'}u'\)
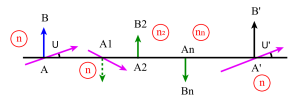
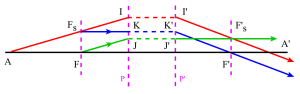
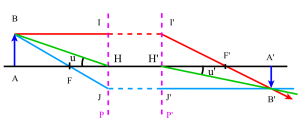
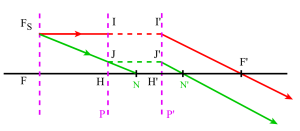
Les plans principaux sont deux plans de front conjugués : le plan principal objet et le plan principal image pour lesquels le grandissement linéaire (ou transversal) est égal à +1.
Relation entre les distances focales objet \(f\) et image \(f'\) :
\(\frac{f'}{f}=-\frac{n'}n\)
La vergence d'un système centré sera défini par :
\(V=\frac{n'}{f'}=-\frac nf\)
Construction de l'image d'un objet plan. On utilisera 2 rayons particuliers :
l'un issu de \(B\) et parallèle à l'axe optique : il émerge après le plan principal image en passant par le foyer image \(F'\)
l'autre issu de \(B\) et passant par le foyer objet \(F\) : il émerge après le plan principal image, parallèle à l'axe optique
Construction de l'émergent correspondant à un incident quelconque. On utilisera les mêmes rayons particuliers que ceux qui ont servi à construire l'image d'un objet \(AB\).
Formules de conjugaison :
Origine aux points principaux :
si : \(\overline{HA}=p\) et \(\overline{H'A'}=p'\) : \(\frac fp+\frac{f'}{p'}=1\) \(\frac{n'}{p'}-\frac np=\frac{n'}{f'}=C\) avec C vergence du système.
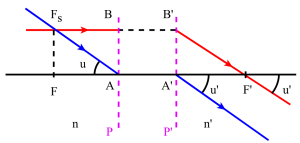
Origine aux foyers: formules de Newton :
si \(\overline{FA}=x\) et \(\overline{F'A'}=x'\) : \(\begin{array}{l}x\cdot x'=f\cdot f'\\\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac fx=-\frac{x'}{f'}\end{array}\)
grandissement angulaire : \(G=\frac{u'}u=\frac n{n'}\frac{\overline{AB}}{\overline{A'B'}}\)
produit du grandissement linéaire par le grandissement angulaire : \(\gamma\cdot G=\frac n{n'}\)
Les plans antiprincipaux sont deux plans conjugués entre lesquels le grandissement est égal à -1. Ce sont les symétriques des plans principaux par rapport aux foyers correspondants (de même pour les plans antiprincipaux).
Les points nodaux \(N\) et \(N'\) sont deux points conjugués, situés sur l'axe, et tels qu'à tout rayon incident passant par le point nodal objet, corresponde un rayon émergent passant par le point nodal image et parallèle au rayon incident.
Les éléments cardinaux d'un système centré comportent: les foyers, les points principaux et antiprincipaux, les points nodaux et antinodaux.
Lorsque pour un système centré donné on connaît deux couples d'éléments cardinaux ou un couple et une distance focale alors le système centré est parfaitement défini.
Solution détaillée
Pour une association de deux lentilles divergentes \(f '_1\) et \(f'_2 < 0\), soit \(f'_1f'_2>0\). La relation \(f'=-\frac{f'_1\cdot f'_2}{\overline{F'_1F_2}}\) montre que \(f '\) est toujours du signe opposé à \(\Delta=\overline{F'_1F_2}>0\) car \(\overline{F'_1F_2}\) toujours positif.
Un système composé de deux lentilles divergentes ne peut donc pas être convergent puisque \(f'=\overline{H'F'}\) sera toujours négatif.
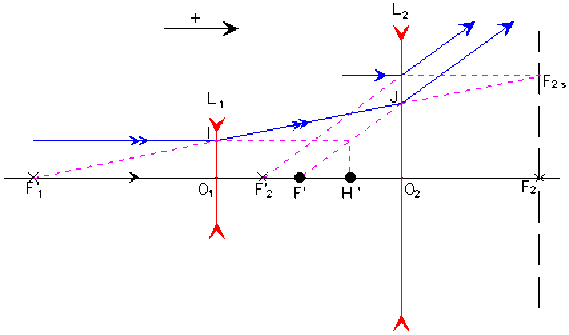
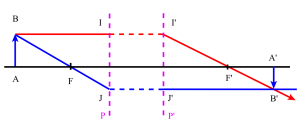
Légende figure :
L'image à l'infini du foyer secondaire objet \(F_{2s}\) donne la direction de l'émergent conjugué du rayon intermédiaire \(IJ\).
Le foyer image \(F'\) de l'association précède le point principal image \(H'\) quel que soit la distance \(O_1O_2\). \(\overline{H'F'}\) sera toujours négatif : Une association de lentilles divergentes ne peut donner un système convergent.