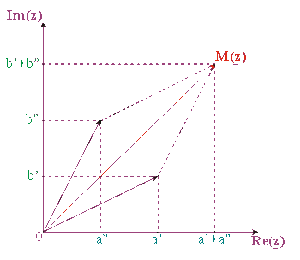Addition
Addition "algébrique"
\(\underline{z}=\underline{z}'+\underline{z}'' \Leftrightarrow a+jb=(a'+jb')+(a''+jb'')=(a'+a'')+j(b'+b'')\Leftrightarrow \left\{\begin{array}{ll} a= a' + a'' \\ b= b' + b'' \end{array}\right.\)
Addition "polaire"
\(\begin{array}{ll}\underline{z} = \underline{z}' + \underline{z}'' \Leftrightarrow \rho(\cos \theta + j \sin \theta) &= \rho'(\cos \theta ' + j \sin \theta') + \rho''(\cos \theta'' + j \sin \theta'') \\ &=(\rho'\cos \theta ' + \rho'' \cos \theta'') + j(\rho'\sin \theta' + \rho'' \sin \theta'') \end{array}\)
Par identification
\(\rho \cos \theta = \rho' \cos \theta' + \rho'' \cos \theta''\)
\(\rho \sin \theta = \rho' \sin \theta' + \rho'' \sin \theta''\)
En élevant au carré et en sommant :
\(\rho^{2} = \rho'^{2} + \rho''^{2} + 2\rho' \rho'' \cos(\theta' - \theta'') \Rightarrow \rho = \sqrt{{\rho'}^{2} + {\rho''}^{2} + 2 \rho' \rho'' \cos(\theta' - \theta'')}\)
Le quotient des expressions précédentes conduit à :
\(\tan \theta = \frac{\rho' \sin \theta' + \rho'' \sin \theta''}{\rho' \cos \theta ' + \rho'' \cos \theta''} \Rightarrow \theta = \arctan \frac{\rho' \sin \theta' + \rho'' \sin \theta''}{\rho' \cos \theta ' + \rho'' \cos \theta''}\)
Addition "vecteur-image"
\(\underline{z}=\underline{z}'+\underline{z}'' \Leftrightarrow \overrightarrow{OM} = \overrightarrow{OM}' + \overrightarrow{OM}''\)
Le "vecteur-image" \(\overrightarrow{OM}\) est égal à la somme vectorielle des "vecteurs-images" \(\overrightarrow{OM'}\) et \(\overrightarrow{OM''}\) représentatifs des nombres complexes \(\underline{z}'\) et \(\underline{z}''\).
De la relation vectorielle nous tirons : \(\overrightarrow{OM'} = \overrightarrow{OM} - \overrightarrow{OM''} = \overrightarrow{M''O} + \overrightarrow{OM} = \overrightarrow{M''M}\)
donc à un vecteur de plan complexe \(\overrightarrow{M''M} = \overrightarrow{OM} - \overrightarrow{OM''}\) on associe l'affixe : \(\underline{z}' = \underline{z} - \underline{z}''\) (affixe de l'extrémité moins affixe de l'origine de ce vecteur)
Remarque : La soustraction se fait par l'addition du nombre complexe opposé. L'opposé de \(\underline{z} = a + jb = \rho~ e^{j\theta}\)
étant
\(-\underline{z} = -a - jb\) pour la forme algébrique
\(-\underline{z} = \rho ~e^{j( \theta + \pi )}\) pour la forme polaire
Conclusion
L'addition de deux nombres complexes sera facilitée, par l'utilisation de la forme algébrique :
Addition des parties réelles
Addition des parties imaginaires
Exemple :
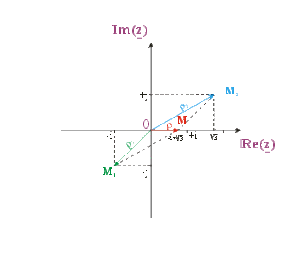
Soient les nombres complexes \(\underline{z_{1}} = -1-j\) et \(\underline{z_{2}}=\sqrt{3}+j\) (formes algébriques)
\(\underline{z_{1}}=\sqrt{2}\left[\cos \frac{5\pi}{4}+j\sin\frac{5\pi}{4}\right]\)
et\(\underline{z_{2}}=2\left[\cos\frac{\pi}{6}+j\sin\frac{\pi}{6}\right]\)(formes trigonométriques)
Addition "algébrique" :
\(\underline{z_{1}} + \underline{z_{2}} = (-1-j) +\sqrt{3}+j = -1 + \sqrt{3}\)
Addition "polaire":
\(\begin{array}{ll}\underline{z_{1}} + \underline{z_{2}} &= \left(\sqrt{2} \cos \frac{5 \pi}{4} + 2 \cos \frac{\pi}{6}\right) + j \left(\sqrt{2} \sin \frac{5 \pi}{4} + 2 \sin \frac{\pi}{6}\right) \\ & = \sqrt{2} \left(\frac{-\sqrt{2}}{2} \right) +2 \left(\frac{\sqrt{3}}{2} \right)+j\left(\sqrt{2}\left(\frac{-\sqrt{2}}{2}\right)+2 . \frac{1}{2}\right)=-1+\sqrt{3} \end{array}\)
Addition "vectorielle":
\(\underline{z}_{1}+\underline{z}_{2} \Leftrightarrow \overrightarrow{OM} = \overrightarrow{OM}_{1} + \overrightarrow{OM}_{2}\)