Nombres complexes

\(\begin{array}{ll}\underline{z}=\frac{\underline{z}'}{\underline{z}''} &\Leftrightarrow a+jb=\frac{a'+jb'}{a''+jb''}=\frac{(a'+jb')(a''-jb'')}{(a''+jb'')(a''-jb'')} = \frac{(a'a''+b'b'')+j(a''b'-a'b'')}{a''^{2} + b''^{2}}\\ \\ &\Leftrightarrow \left\{\begin{array}{ll} a= \frac{a'a'' + b'b''}{{a''}^{2}+{b''}^{2}} \\ \\ b= \frac{a''b' - a'b''}{{a''}^{2}+{b''}^{2}} \end{array}\right. \end{array}\)

\(\begin{array}{ll}\underline{z} = \frac{\underline{z}'}{\underline{z}''} \Leftrightarrow \rho(\cos \theta + j \sin \theta) & = \frac{\rho'(\cos \theta ' + j \sin \theta')} {\rho''(\cos \theta'' + j \sin \theta'')} = \frac{\rho'}{\rho''}(\cos \theta' + j \sin \theta')(\cos \theta'' - j \sin \theta'')\\ & =\frac{\rho'}{\rho''}\left[\left(\cos \theta'\cos\theta''+\sin\theta'\sin\theta''\right)\right. + \\& \left.j \left(\sin \theta'\cos\theta''-\cos\theta'\sin\theta''\right)\right] \\ & = \frac{\rho'}{\rho''}\left[\cos(\theta' - \theta'') + j \sin(\theta' - \theta'')\right]\end{array}\)

\(\rho e^{j \theta} = \frac{\rho' e^{j \theta'}}{ \rho'' e^{j \theta''}} = \frac{\rho'}{\rho''} e^{j(\theta'-\theta'')}\Leftrightarrow \left\{\begin{array}{ll} \rho = \frac{\rho'}{\rho''} \\ \theta = \theta' - \theta'' \end{array}\right.\)

Des résultats de la division "polaire", diviser le nombre complexe \(\underline{z}'\), de vecteur-image \(\overrightarrow{OM}'\) par le nombre complexe \(\underline{z}''\) de module \(\rho''\) et d'argument \(\theta''\) consiste à faire subir au "vecteur-image" \(\overrightarrow{OM}'\) une rotation d'angle \(-\theta''\) et une division de son module par \(\rho''\).

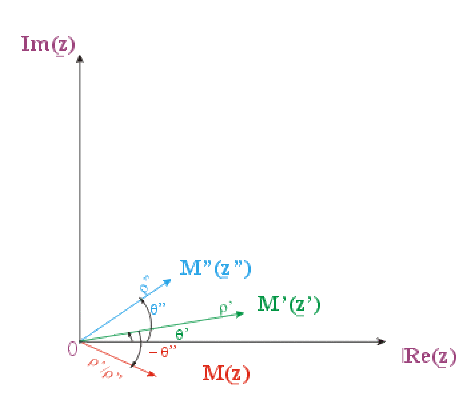
Conclusion

De nouveau la forme polaire est préférée dans le cas de la division de deux nombres complexes

• Division des modules

• Soustraction des arguments