Chaleur de combustion
Certaines réactions sont si courantes qu'on a donné un nom particulier à leur enthalpie de réaction ; c'est le cas des réactions de combustion.
Définition : Chaleur de combustion.
On appelle chaleur de combustion \(\mathbf{\Delta_\textrm{comb}H^{\circ}_{298}}\) le \(\Delta_\textrm rH^{\circ}_{298}\) de la réaction complète d'une mole d'un corps pur avec le dioxygène.
La combustion conduisant toujours au degré d'oxydation le plus élevé, la combustion d'un composé organique par exemple correspondra à sa transformation en \(\textrm{CO}_2\) et \(\textrm H_2\textrm O\). Quand un composé contient l'élément azote, sa combustion le transforme en \(\textrm{CO}_2\) , \(\textrm N_2\), et \(\textrm H_2\textrm O\).
L'application de la loi de Hess à des cycles judicieusement choisis permet de calculer les \(\Delta_\textrm rH^{\circ}_{298}\) de transformations ne faisant pas intervenir \(\textrm O_2\) par simple addition et soustraction de chaleurs de combustion.
Exemple : Calcul utilisant les enthalpies de combustion
Calculer l'enthalpie standard de formation de l'aniline (\(\textrm C_6\textrm H_5\textrm{NH}_2\)) liquide à partir des données suivantes :
composé | \(\mathrm{C (s)}\) | \(\mathrm{H_2 (g)}\) | \(\mathrm{aniline (l)}\) |
\(\mathrm{\Delta_{comb}~H°_{298} (kJ.mol^{-1})}\) | - 395 | - 286 | - 3402 |
Solution non détaillée
\(\Delta_\textrm f H^{\circ}_{298\textrm{ aniline (liq)}} = 31\textrm{ kJ.mol}^{-1}\)
Solution détaillée
L'enthalpie standard de formation \(\Delta_\textrm f H^{\circ}_{298}\) de l'aniline correspond à l'enthalpie standard de la réaction :
\(6.\textrm{C (s)} + \frac{7}{2}.\textrm H_2\textrm{ (g)} + \frac{1}{2}.\textrm N_2\textrm{ (g)}\to \textrm C_6\textrm H_5\textrm{NH}_2\textrm{ (liq)}\) .
Les trois réactions de combustion sont : \(\textrm{C (s)} + \textrm O_2\textrm{ (g)}\to \textrm{CO}_2\textrm{ (g)}\) , \(\textrm H_2\textrm{ (g)} + \frac{1}{2}.\textrm O_2\textrm{ (g)}\to\textrm H_2\textrm{O (liq)}\)
et \(\textrm C_6\textrm H_5\textrm{NH}_2\textrm{ (liq)} + \frac{31}{4}.\textrm O_2\textrm{ (g)}\to 6.\textrm{CO}_2\textrm{ (g)} +\frac{7}{2}.\textrm H_2\textrm{O (liq)} +\frac{1}{2}.\textrm N_2\textrm{ (g)}\)
Pour calculer \(\Delta_\textrm f H^{\circ}_{298}\) de l'aniline, il faut imaginer un cycle dans lequel ne figurent que les réactions de combustion ci-dessus et la réaction de formation de l'aniline.
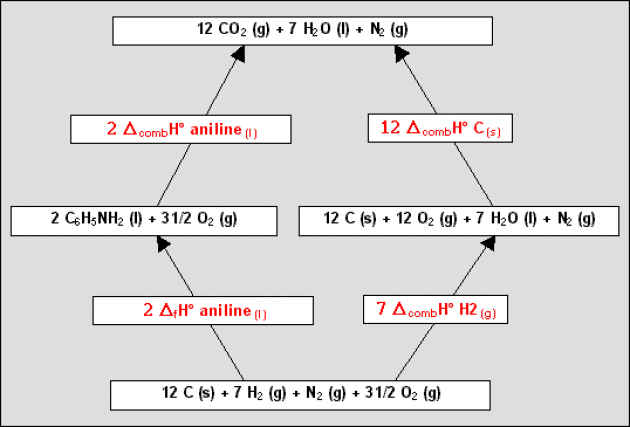
Par exemple, on peut concevoir le cycle ci-contre partant des corps simples et aboutissant aux produits de combustion.
On aura alors : \(2.\Delta_\textrm f H^{\circ}_{298\textrm{ aniline}} = 7. \Delta_\textrm{comb}H^{\circ}_{298\textrm{ H}_2} + 12. \Delta_\textrm{comb}H^{\circ}_{298\textrm{ C}} - 2. \Delta_\textrm{comb}H^{\circ}_{298\textrm{ aniline}}\)
On trouve \(\Delta_\textrm f H^{\circ}_{298\textrm{ aniline (liq)}} = 31\textrm{ kJ.mol}^{-1}\).