Cycles avec changement d'état physique d'un ou plusieurs composés
Le calcul d'un \(\Delta_\textrm rH^{\circ}_T\) à partir d'un \(\Delta_\textrm rH^{\circ}_{298}\) s'effectue en appliquant la loi de Kirchhoff ; cette dernière n'est applicable que dans un intervalle de température à l'intérieur duquel il n'y a pas de changement d'état physique des réactifs ou des produits.
S'il y a un changement d'état, il convient de tenir compte de l'énergie fournie où reçue lors de cette transformation physique à la température \(T_e\) et de la discontinuité dans la variation du \(C_p\) de l'espèce chimique concernée.
On effectue les calculs en imaginant un cycle comprenant une première étape entre 298 K et \(T_e\), une seconde correspondant au changement d'état à \(T_e\), une troisième entre \(T_e\) et \(T\).
Exemple : Calcul d'enthalpie de réaction avec changement d'état physique
A partir des tables d'enthalpies de formation, calculez l'enthalpie de réaction à 500 K de la réaction
\(\mathbf{\textrm I_2\textrm{ (g)}+\textrm H_2\textrm{ (g)}=2.\textrm{HI (g)}}\)
\(\mathrm{H_2(gaz)}\) | \(\mathrm{I_2 (solide)}\) | \(\mathrm{I_2 (gaz)}\) | \(\mathrm{HI (gaz)}\) | |
\(\mathrm{\Delta_f H°_{298}~ en~ kJ. mol^{-1}}\) | 0 | 0 | 62,43 | 26,48 |
valeur moyenne de \(\mathrm{Cp~en ~J.mol^{-1}.K^{-1}}\) | 29 | 23,4 | 37,6 | 38,3 |
Solution non détaillée
\(\Delta_\textrm rH^{\circ}_{500}=-\textrm{7,05 kJ.mol}^{-1}\)
Solution détaillée
Les données des tables nous fournissent \(\Delta_\textrm rH^{\circ}_{298}\) pour la réaction\( \textrm I_2\textrm{ (s)} + \textrm H_2\textrm{ (g)} = 2.\textrm{HI (g)}\) .
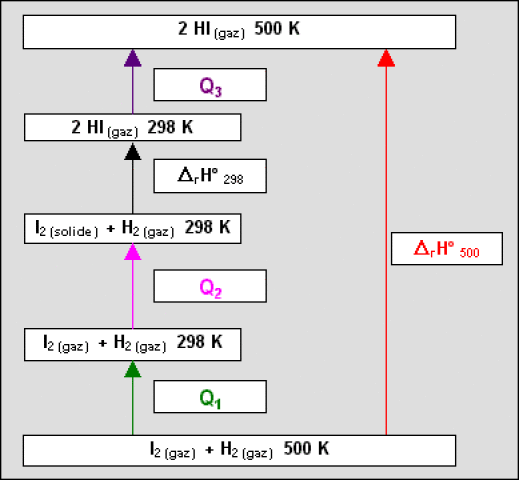
Le cycle ci-contre nous montre que :
\(\Delta_\textrm rH^{\circ}_{500}=\Delta_\textrm rH^{\circ}_{298}+Q_1+Q_2+Q_3\) avec
\(Q_1=(C_{p \textrm I_2\textrm{ (g)}}+C_{p \textrm H_2\textrm{ (g)}}).(298-500)\)
\(Q_2=-\Delta_\textrm{subl}H^{\circ}_{298 \textrm I_2}=-\Delta_\textrm fH^{\circ}_{298 \textrm I_2\textrm{ (g)}}\)
\(Q_3=(2.C_{p \textrm{HI}\textrm{ (g)}}).(500-298)\)
et
\(\Delta_\textrm rH^{\circ}_{298} = 2. \Delta_\textrm f H^{\circ}_{298\textrm{ HI (g)}} = \textrm{52,96 kJ.mol}^{-1}\)
Les expressions de \(Q_1\) et \(Q_3\) supposent les \(C_p\) indépendants de la température.
Remarquez que nous n'avons pas utilisé la température de sublimation du diiode dans ces calculs.
On trouve finalement \(\Delta_\textrm rH^{\circ}_{500} = - \textrm{7,05 kJ.mol}^{-1}\) .