Cinética química

Curso
Herramientas

Conceptos fundamentales de la cinética química
- Curso

Avance de reacción

Definición :

Para poder estudiar la evolución de la reacción en función del tiempo y no conformarse con conocer su estado inicial y su estado final, hay que definir su avance con precisión en todo momento. Si tenemos 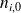moles de 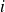en el momento inicial 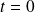y 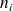moles en el momento 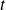, definimos el avance de la reacción en ese momento 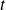con:

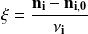
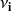es el coeficiente estequiométrico de 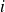(con el signo + para los productos y el signo – para los reactantes).

Cuando la sustancia considerada es un reactante, su cantidad disminuye durante la reacción. Por lo tanto 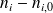es negativo. Por convención, se asigna el coeficiente estequiométrico 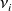con el signo menos; como resultado, el avance de la reacción 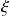es positivo.
Cuando la sustancia considerada es un producto ( 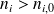), su cantidad aumenta durante la reacción. Por lo tanto, 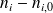es positivo. El coeficiente estequiométrico 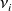tiene el signo más; como resultado, el avance de la reacción 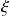es positivo.

Consejo :

Como su nombre lo indica, el valor de avance de la reacción aumenta 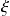cuando la reacción avanza.
La dimensión de 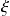es la de una cantidad de materia, por lo tanto, es una magnitud extensiva. La unidad en el sistema internacional es el mol.
El valor de avance de la reacción 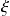no depende de la elección de la sustancia (reactivo o producto) utilizada para calcularlo (por otra parte, es su principal interés).
En la práctica, para calcular el avance de la reacción, utilizamos la sustancia más fácil de dosificar. Pero ATENCIÓN, esto solo es así si la reacción es la única que deja intervenir los reactivos y los productos considerados (decimos que la reacción es aislada) y si no hay productos intermedios formados.
El hecho de que el avance sea de una magnitud extensiva tiene como consecuencia que, para una misma cantidad de materia transformada, el valor de 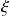depende de los coeficientes estequiométricos, por lo tanto, de la manera de escribir la ecuación química.

Nota: esta noción de avance de la reacción está desarrollada en el módulo: "Termodinámica química".

Ejemplo : El valor de avance de la reacción no depende de la elección de la sustancia (reactante o producto) utilizada para calcularlo

Consideremos la reacción de combustión del etano:

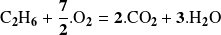
Consideremos al principio, 3 moles de etano en un exceso de oxígeno molecular.

Calculemos el avance 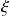de la reacción cuando 2 moles de etano reaccionaron. Primeramente, hagamos el cálculo para el etano. Cuando 2 moles de etano se han consumiedo, queda 1 mol de etano.

Donde:

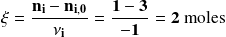
Ahora, hagamos el cálculo para el oxígeno molecular. La cantidad de oxígeno molecular consumido es igual a la cantidad de etano (2 moles) que reaccionaron, multiplicado por , o sea: .

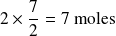Donde:

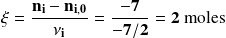
Por lo tanto, encontramos el mismo grado de avance de la reacción, sea cual sea la sustancia elegida para calcularlo.

Encontraríamos el mismo resultado haciendo el cálculo con los productos.

Cálculo con :

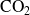La cantidad de 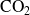formada es igual al doble de la cantidad de etano desaparecida, es decir, .

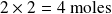Donde

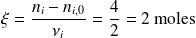
Cálculo con :

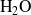La cantidad de 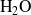formada es el triple de la cantidad de etano desaparecida, es decir, .

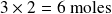Donde

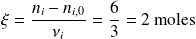
Ejemplo : Cuando una sustancia (reactante o producto) interviene en varias reacciones, el grado de avance depende de la elecciónde la sustancia de la sustancia utilizada para calcularlo.

Cuando una reacción es aislada, el grado de avance de la reacción no depende de la elección de la sustancia (reactante o producto) utilizada para calcularlo. Esto no es así cuando un mismo reactante (o producto) interviene en varias reacciones que ocurren simultáneamente. Por ejemplo, consideremos el caso de la combustión de una mezcla de metano y etano. Las dos reacciones ocurren simultáneamente y pueden escribirse:

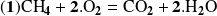
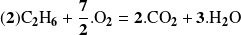
Para calcular el avance de las dos reacciones, hay que conocer las cantidades transformadas de los reactantes o de los productos. Por ejemplo, una mezcla de 0,5 moles de metano 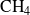y de un mol de etano 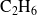que reaccionan completamente en un exceso de oxígeno. Las cantidades transformadas son:

	CH₄	C₂H₆	O₂	CO₂	H₂O
n_i - n_{i, 0}	- 0,5	- 1,0	- 4,5	2,5	4,0

Trate de encontrar estos resultados intermedios usted mismo.

Si sabe encontrar estos valores, pase al cálculo del avance de las reacciones.

Si no logra encontrar estos valores, proceda en varias etapas, tratando de completar el cuadro que aparece más abajo. Efectivamente, para calcular las cantidades transformadas, es útil llenar un cuadro con las cantidades iniciales ( 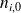), restantes ( 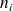) et ( 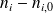) transformadas de cada sustancia:

	CH₄	C₂H₆	O₂	CO₂	H₂O
n_i,0
n_i
n_i - n_i,0

Haga clic en el avance para obtener el detalle del modo de cálculo de las reacciones... pero tómese el tiempo para tratar de encontrar estos resultados...

Cabe destacar que ciertos reactivos participan solamente en una sola de las dos reacciones.

Es el caso del metano 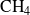en la primera reacción y del etano 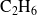en la segunda. Por lo tanto, es posible calcular separadamente el avance de cada reacción basándose únicamente en las cantidades transformadas de estos reactivos.

Para la reacción (1), obtenemos:

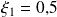
Para la reacción (2), obtenemos:

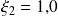
En los compuestos que participan en las dos reacciones, es fácil relacionar su cantidad transformada con los grados de avance de ambas reacciones:

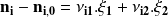
Apliquemos esta relación a los otros componentes del sistema, evidentemente, encontramos los valores calculados anteriormente.

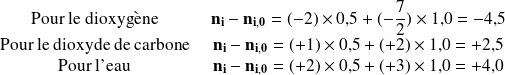
Ejemplo : Dado que el grado de avance de la reacción es de una magnitud extensiva, su valor depende de la escritura de la ecuación balanceada.

Consideremos, por ejemplo, una mezcla compuesta de un mol de acetileno y dos moles de oxígeno molecular

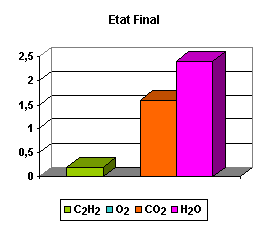
Calculemos el grado de avance de la reacción cuando la reacción ha terminado.

La ecuación balanceada de la reacción puede escribirse:

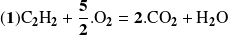
Pero también puede escribirse:

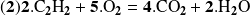
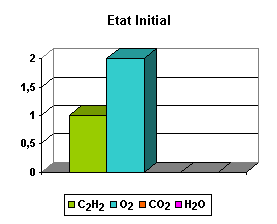
Calculemos el grado de avance de la reacción cuando la reacción ha terminado.

Con la ecuación (1), encontramos:

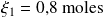
Con la ecuación (2), encontramos:

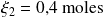
Para calcular el grado de avance 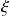necesitamos conocer las cantidades transformadas de cada sustancia. Evidentemente, estas cantidades no dependen de la escritura de la ecuación balanceada. Pero no sucede lo mismo con el avance 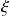ya que, para una misma sustancia, los coeficientes estequiométricos son diferentes en las dos ecuaciones. Trate de encontrar usted mismo los valores de 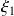y .

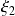Para calcular el grado de avance, primero hay que determinar las cantidades transformadas de cada sustancia. Encontramos las cantidades transformadas siguientes:

	C₂H₂	O₂	CO₂	H ₂O
n_i - n_i,0	- 0,8	- 2,0	+ 1,6	+ 0,8

Si desea obtener detalles acerca de estos cálculos de las cantidades transformadas entre aquí^[1] .

Las cantidades de sustancias transformadas (por lo tanto, las cantidades restantes) no dependen de la manera en que escribimos la ecuación balanceada. Pero no ocurre lo mismo en el caso del avance de la reacción, ya que los coeficientes estequiométricos para cada sustancia son diferentes en las dos ecuaciones.

Retomemos el cuadro de las cantidades de sustancias transformadas:

	C₂H₂	O₂	CO₂	H ₂O
n_i - n_i,0	- 0,8	- 2,0	+ 1,6	+ 0,8

Calcule el avance de la reacción utilizando la ecuación balanceada:

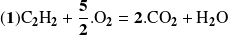
Ahora, retome el cálculo con la ecuación:

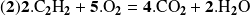
Entre aquí^[2] para ver los resultados. Encontramos 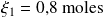con la ecuación (1) y 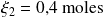con la ecuación (2). Puede ver que, para las mismas cantidades de materia transformadas, el grado de avance de la reacción depende de la manera en que escribimos la ecuación balanceada. Esto es normal, ya que la expresión del avance hace intervenir los coeficientes estequiométricos, los cuales dependen de la ecuación balanceada.

En conclusión:

El grado de avance de una reacción no depende del componente elegido para calcularlo, sino de la escritura de la ecuación balanceada. Por lo tanto, no podemos disociar el grado de avance de una reacción de la ecuación balanceada que sirvió para calcularlo.

Cálculo de las cantidades transformadas
Podemos hacer el cálculo de las cantidades transformadas en forma indistinta con las dos ecuaciones balanceadas \mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}Hagamos el cálculo con la ecuación (1)Las cantidades iniciales n_{\textrm C_2\textrm H_{2,0} = \textrm{1,0 mol}}, n_{\textrm O_{2,0}} = \textrm{2,0 moles} no están en las proporciones estequiométricas.\mathbf{\frac{n_{\textrm C_2\textrm H_{2,0}}}{n_{\textrm O_{2,0}}}=\frac{\textrm{1,0}}{\textrm{2,0}}=\textrm{0,5}>\frac{\textrm v_{\textrm C_2\textrm H_2}}{\textrm v_{\textrm O_2}}=\frac{-1}{-5/2}=\textrm{0,4}}Hay un exceso de acetileno con respecto a la cantidad de oxígeno molecular disponible. Cuando la reacción se haya completado, todo el oxígeno molecular se habrá consumido, donde, en el caso del oxígeno molecular, la cantidad transformada es n_i – n_{i,0} = 0 – 2 = -\textrm{2,0 moles}. La cantidad de acetileno consumida se deduce de la cantidad de oxígeno molecular disponible: \mathbf{\frac{\textrm C_2\textrm H_{2,\textrm{consommé}}}{-1}=\frac{\textrm O_{2,\textrm{consommé}}}{-2/5}}Donde la cantidad de acetileno transformada = 2/5 \times (–\textrm{2,0}) = – \textrm{0,8 moles}. La cantidad de dióxido de carbono formada es el doble de la cantidad de acetileno desaparecida, o sea 2 \times \textrm{0,8} = \textrm{1,6 moles}. La cantidad de agua formada es igual a la cantidad de acetileno desaparecida, o sea, 0,8 mol. Ahora, hagamos el cálculo con la ecuación (2)\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}Las cantidades iniciales n_{\textrm C_2\textrm H_{2,0} = \textrm{1,0 mol}} y n_{\textrm O_{2,0}} = \textrm{2,0 moles} no están en las proporciones estequiométricas: \mathbf{\frac{n_{\textrm C_2\textrm H_{2,0}}}{n_{\textrm O_{2,0}}}=\frac{\textrm{1,0}}{\textrm{2,0}}=\textrm{0,5}>\frac{\textrm v_{\textrm C_2\textrm H_2}}{\textrm v_{\textrm O_2}}=\frac{-2}{-5}=\textrm{0,4}}por lo tanto, hay un exceso de acetileno con respecto a la cantidad de oxígeno disponible. Cuando la reacción se haya completado, todo el oxígeno molecular se habrá consumido, donde, en el caso del oxígeno molecular, la cantidad transformada es n_i – n_{i,0} = 0 – 2 = -\textrm{2,0 moles}. La cantidad de butano consumido se deduce de la cantidad de oxígeno molecular: \mathbf{\frac{\textrm C_2\textrm H_{2,\textrm{consommé}}}{-2}=\frac{\textrm O_{2,\textrm{consommé}}}{-5}}Donde la cantidad de acetileno transformada es \mathbf{\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{4}{2}=2}La cantidad de dióxido de carbono formada es el doble de la cantidad de acetileno desaparecida, o sea 2\times \textrm{0,8} = \textrm{1,6 moles}. La cantidad de agua formada es el triple de la cantidad de acetileno desaparecida, o sea 2 \times \textrm{0,8} = \textrm{2,4 moles}.
Cálculo del avance
Podemos hacer el cálculo del avance de la reacción a partir de cualquier compuesto de una ecuación balanceada \mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}Con la ecuación (1) a partir del acetileno \mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{0,8}}{-1}=\textrm{0,8 moles}}a partir del oxígeno molecular\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{2,0}}{-5/2}=\textrm{0,8 moles}}a partir del dióxido de carbono\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{1,6}}{2}=\textrm{0,8 moles}}a partir del agua\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{0,8}}{1}=\textrm{0,8 moles}}Con la ecuación (2) a partir del acetileno \mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{0,8}}{-2}=\textrm{0,4 moles}}a partir del oxígeno molecular\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{2,0}}{-5}=\textrm{0,4 moles}}a partir del dióxido de carbono\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{1,6}}{4}=\textrm{0,4 moles}}a partir del agua\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{0,8}}{2}=\textrm{0,4 moles}}

Inicio

Imprimir