Noción de conjunto
Noción de conjunto:
Desde principios del siglo, todos los objetos matemáticos se han descrito utilizando el lenguaje de los conjuntos. Conjuntos de números, conjuntos de puntos, conjuntos de funciones, etc...
No se define el concepto de conjunto. Simplemente, especificaremos las notaciones y las reglas para utilizar este lenguaje de forma segura.
Ejemplo :
Usted mismo ha comenzado a utilizar este lenguaje.
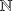conjunto de enteros naturales,
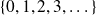
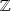conjunto de enteros relativos,
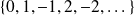
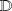conjunto de los decimales, es decir, números que pueden escribirse bajo la forma
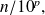
y
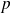enteros relativos. Los decimales incluyen los enteros y los números que pueden escribirse bajo una forma decimal con un número finito de cifras no nulas después de la coma. Se deberá tener cuidado de que los números decimales tienen dos escrituras decimales ilimitadas: una con ceros indefinidamente a partir de un cierto rango, la otra con
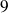indefinidamente a partir de un cierto rango. Por ejemplo:
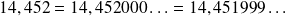
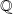conjunto de los racionales, es decir, números que pueden escribirse como el cociente de dos enteros
y
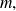
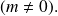Se admite que a todo número racional se asocia un desarrollo decimal periódico, único si el número no es un decimal.
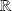los números reales. Éstos no han sido definidos hasta ahora. Este año se dará de manera muy precisa las propiedades de los números reales utilizables en las demostraciones. A todo número racional se asocia un desarrollo decimal ilimitado, único si el número no es un decimal.
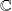los números complejos que pueden escribirse bajo la forma
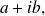con
y
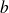reales.
Usted ha utilizado también este lenguaje en geometría hablando de la recta como un conjunto de puntos, etc.
Noción de pertenencia
:
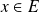es un elemento del conjunto
:
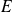
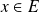pertenece al conjunto
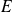
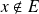: es la negación de
:
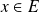
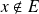no es un elemento del conjunto
:
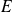
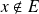no pertenece al conjunto
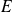
Conjunto vacío
Se considera en matemáticas, que hay un único conjunto, denominado conjunto vacío, que no contiene ningún elemento, y que representa
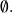Si se considera un elemento
cualquiera, se tiene necesariamente
Conjuntos infinitos
Los conjuntos se crearon para manejar conjuntos infinitos. Cuando, a finales del siglo XIX, los matemáticos comenzaron a manejar conjuntos, se dieron cuenta que la noción de "conjunto de todos los conjuntos" conducía a contradicciones. A fin de limitar los conjuntos utilizados, se han fijado la regla siguiente de formación de conjuntos.
Regla de formación
Si se da un conjunto
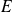y una propiedad
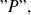se puede formar un nuevo conjunto
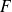constituido por elementos de
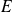que cumplen la propiedad
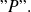Esto se escribe:
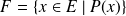
Escritura de un conjunto
Hay dos posibilidades para escribir un conjunto:
Escritura en extensión
Se enumera sus elementos. Se dice que se define el conjunto en extensión. Esta definición no siempre se puede utilizar: ¿cómo escribir así conjuntos tales como el conjunto de puntos de un segmento, por ejemplo?
Ejemplos:
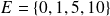
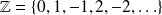
Escritura en comprensión
Se da una propiedad que caracteriza sus elementos. Se dice que se define el conjunto en comprensión. Es la escritura de conjuntos más utilizada.
Ejemplo :
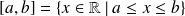
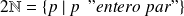
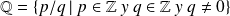
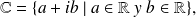con
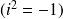
Observación :
Hay dos partes en la escritura de un conjunto, separadas por una barra vertical.
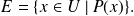
La primera
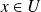indica dónde se han tomado los elementos del conjunto, la segunda
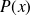indica una propiedad característica de los elementos del conjunto
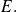Los signos lógicos solo pueden entonces intervenir eventualmente a nivel de la escritura de la propiedad
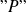y, en ningún caso, en la primera parte de la escritura.
