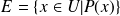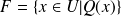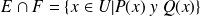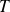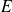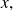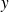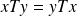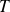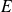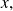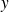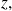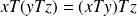Intersección de conjuntos
Si
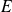y
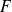son conjuntos,
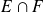es el conjunto constituido por elementos que pertenecen al mismo tiempo a los dos conjuntos
y
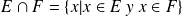
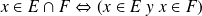
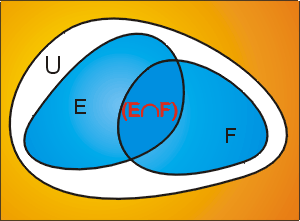
Se puede, a modo de ejercicio, demostrar estas propiedades, así como las siguientes.
Enlace con las leyes de Morgan
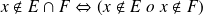
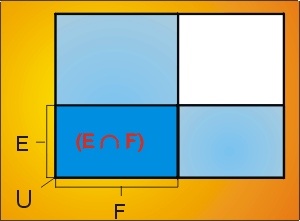
dicho de otro modo:
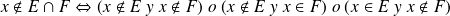
Propiedades de la intersección
La intersección de dos conjuntos
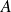y
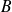es el mayor conjunto que contiene a la vez estos dos conjuntos
Lo que se traduce en lenguaje formalizado por la conjunción de dos propiedades.
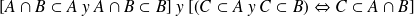
Idempotencia
Para todo conjunto
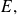se tiene
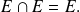
Conmuta[1]tividad [1]
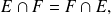para todos los conjuntos
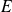y
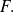
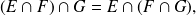para todos los conjuntos
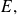
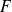y
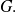Esto permite definir la intersección de tres conjuntos, de un número finito de conjuntos.
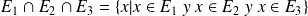
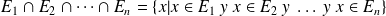
Generalización
La intersección se generaliza a una intersección cualquiera de una familia de conjuntos indexada por un conjunto no vacío
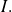
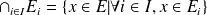
(El sentido del símbolo
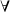que quiere decir "para todo" se revisará a continuación.)
Enlace con el conector "y"
Supongamos el conjunto
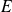definido por una propiedad
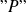y el conjunto
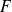definido por una propiedad
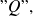entonces, se observa que el conjunto
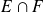está definido por la propiedad
:
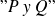