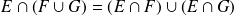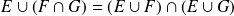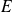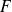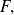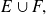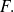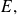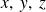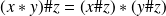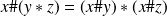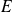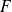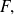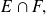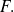Propiedad de distributividad
La intersección es distributiva[2] en relación a la unión[1] Esto resulta de la distributividad de la conjunción en relación con la disyunción.
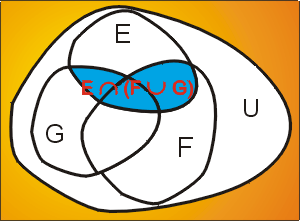|  prop_distr |
Demostración :
Primera indicación
Para demostrar una igualdad de conjuntos se deben demostrar dos inclusiones:
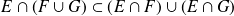
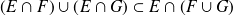
Para demostrar una inclusión de conjuntos, se ve si se pueden utilizar propiedades conocidas, de lo contrario, se toma un elemento del primer conjunto y se demuestra que pertenece al segundo.
Segunda indicación
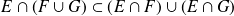
Para demostrar esta inclusión, tomar un elemento de
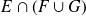y demostrar que éste pertenece a
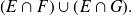
Se comienza, entonces, por «sea
»
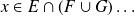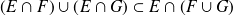
Para demostrar esta inclusión, utilizar propiedades conocidas de la intersección y de la unión de conjuntos.
Demostración detallada
Primera inclusión
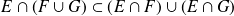
Sea
un elemento de
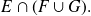El elemento
pertenece a la vez a
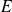y a
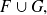entonces
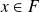o
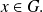Encontramos dos casos posibles:
Primer caso:
pertenece a
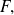entonces a
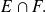Como
es un subconjunto de
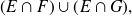esto demuestra que
es elemento de
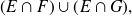como queríamos demostrar.Segundo caso:
pertenece a
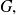entonces a
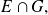subconjunto de
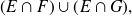esto demuestra que
es elemento de
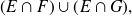como queríamos demostrar.Conclusión: Por consiguiente se ha demostrado que todo elemento de
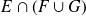es elemento de
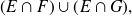y, por lo tanto, la inclusión buscada.
Segunda inclusión
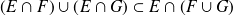
Para demostrar esta inclusión, se utilizará la propiedad conocida de la unión de dos conjuntos (que es el conjunto más pequeño conteniendo a los dos).
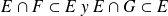
entonces:
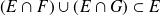
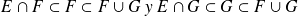entonces,
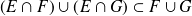
Se utiliza ahora la propiedad conocida de la intersección de dos conjuntos (que es el mayor conjunto contenido en ambos). Puesto que
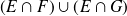es un subconjunto tanto de
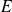como de
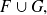estará incluido en la intersección de
:
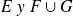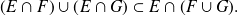
La unión es distributiva en relación con la intersección [3] Demostrar esta propiedad utilizando los mismos métodos que en la demostración anterior.
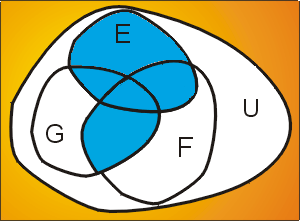|  prop_distr2 |
