Inclusión e igualdad
Inclusión de conjuntos
Se dice que un conjunto
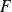 se incluye en un conjunto
se incluye en un conjunto
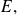 si todo elemento de
si todo elemento de
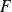 pertenece a
pertenece a
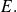
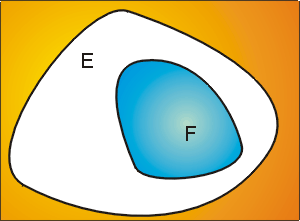

La inclusión es una inclusión amplia
De acuerdo con la definición anterior, todo conjunto
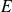 se incluye en sí mismo.
se incluye en sí mismo.
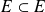
Inclusión estricta
Cuando el subconjunto
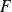 está estrictamente incluido en el conjunto
está estrictamente incluido en el conjunto
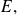 se dice que
se dice que
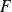 es un subconjunto propio de
es un subconjunto propio de
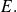 Se debe entonces precisarlo mediante la conjunción de las dos propiedades:
Se debe entonces precisarlo mediante la conjunción de las dos propiedades:
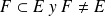
Conjunto vacío e inclusión
El conjunto vacío está contenido en todo el conjunto
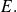
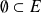
Un conjunto
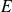 no vacío tiene, entonces, siempre al menos dos subconjuntos, el conjunto vacío y él mismo. Por el contrario, el conjunto
no vacío tiene, entonces, siempre al menos dos subconjuntos, el conjunto vacío y él mismo. Por el contrario, el conjunto
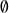 tiene un único subconjunto, él mismo.
tiene un único subconjunto, él mismo.
Ejemplos de inclusión de conjuntos
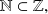
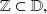
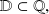
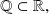
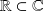
Sea el conjunto
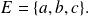 Sus subconjuntos son los conjuntos:
Sus subconjuntos son los conjuntos:
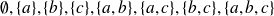
Transitividad de la inclusión:
Siendo
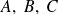 tres conjuntos, si el primer conjunto
tres conjuntos, si el primer conjunto
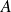 está contenido en el segundo
está contenido en el segundo
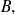 si el segundo conjunto
si el segundo conjunto
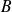 está contenido en el tercero
está contenido en el tercero
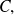 entonces, el primer conjunto
entonces, el primer conjunto
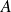 está contenido en el tercero
está contenido en el tercero
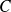 ; se dice que la inclusión es transitiva; esta propiedad se enuncia:
; se dice que la inclusión es transitiva; esta propiedad se enuncia:
Si
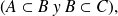 entonces
entonces

y se escribe en lenguaje formalizado donde
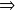 se lee "implica" y será revisado a continuación:
se lee "implica" y será revisado a continuación:
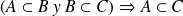
Justificación
Sea
 un elemento de
un elemento de
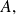 de acuerdo con la hipótesis
de acuerdo con la hipótesis
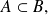 se puede afirmar que
se puede afirmar que
 es elemento de
es elemento de
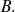 De acuerdo con la hipótesis
De acuerdo con la hipótesis
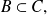 se puede afirmar que
se puede afirmar que
 es elemento de
es elemento de
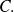 Se ha demostrado entonces que todo elemento de
Se ha demostrado entonces que todo elemento de
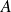 es elemento de
es elemento de
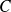 y que entonces
y que entonces
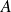 está incluido en
está incluido en
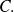
Abuso de escritura
Se puede escribir una serie de inclusiones que pone en evidencia la transitividad de la inclusión:
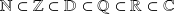
Igualdad de conjuntos:
Dos conjuntos
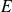 y
y
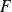 son iguales si tienen exactamente los mismos elementos. Esto se traduce por dos inclusiones simultáneas.
son iguales si tienen exactamente los mismos elementos. Esto se traduce por dos inclusiones simultáneas.