Demostraciones
¿Cómo demostrar?
Una inclusión
Para demostrar que un conjunto
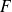está incluido en un conjunto
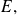se toma un elemento
cualquiera de
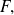se utilizan las hipótesis que definen el conjunto
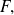y se demuestra que
cumple las propiedades que definen el conjunto
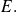La demostración toma, entonces, la estructura siguiente:
Sea
un elemento del conjunto
...
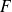
(razonamiento)
...
entonces
es un elemento del conjunto
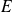
Conclusión:
Una no-inclusión
¿Cómo probar
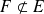? Basta encontrar un elemento de
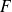que no está en el conjunto
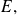(un contra-ejemplo es suficiente).
Una igualdad de conjuntos
Dos conjuntos son iguales si tienen exactamente los mismos elementos. Esto se traduce por dos inclusiones simultáneas.
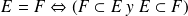
Para demostrar la igualdad de dos conjuntos
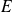y
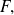será necesario hacer dos demostraciones de inclusión, por una parte para demostrar
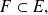y por otra parte para demostrar
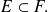
Utilizar en una demostración
Una inclusión
¿Cómo utilizar una hipótesis
en una demostración? Se establece que todo elemento que pertenece a
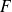pertenece también a
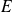y entonces cumple las propiedades que definen
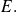
Una no-inclusión
¿Cómo utilizar una hipótesis
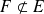? Se afirma la existencia de al menos un elemento de
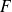que no es elemento de
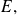se toma dicho elemento y se utiliza en la demostración que sigue.
Ejemplo :
Retomamos la demostración de la propiedad realizada anteriormente:
Si
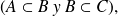entonces
La justificación ha seguido los esquemas "Demostrar una inclusión" y "utilizar una inclusión".
"Demostrar una inclusión"
El objetivo es demostrar que
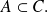Se ha tomado entonces un elemento
de
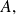y tenemos como objetivo demostrar que
es elemento de
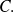
"Razonamiento"
Consiste en utilizar dos inclusiones dadas como hipótesis,
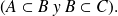
"Utilizar una inclusión": utilizando la inclusión
dada por hipótesis, se puede afirmar que
es elemento de
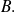
"Utilizar una inclusión
": como
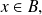utilizando la inclusión
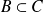dada por hipótesis, se puede afirmar que
es elemento de
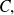lo que es nuestro objetivo.
"Concluir"
Se ha demostrado entonces que todo elemento de
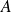es elemento de
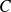y por lo tanto, que
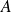está incluido en
