Ensembles particuliers
Ensemble des parties d'un ensemble
Pour tout ensemble \(E,\) on peut former un ensemble que l'on note \(\color{red}P\color{black}(E),\) dont les éléments sont les sous-ensembles de \(E.\)
\(\color{red}P\color{black}(E) = \{F | F \subset E\}\)
\(F\in \color{red}P\color{black}(E)\Leftrightarrow F\subset E\)
Exemple : 1
Pour l'ensemble \(E = \{a, b, c\},\) l'ensemble des parties est
\(\color{red}P\color{black}(E) = \{\emptyset, \{a\},\{b\}, \{c\},\{a, b\}, \{a, c\}, \{b, c\},\{a, b, c\}\}\)
Attention : à bien distinguer
\(a\) qui désigne un élément de \(E,\) et \(\{a\}\) qui désigne le sous-ensemble de \(E,\) appelé singleton, qui ne contient que l'élément \(a.\) On écrira :
\(a\in E~~ ;~~ \{a\}\subset E~~ ;~~ \{a\}\in \color{red}P\color{black}(E)\)
\(a\in \{a\}\)
Exemple :
\(\color{red}P\color{black}(\emptyset) = \{\emptyset\},\) \(\color{red}P\color{black}(\emptyset)\) est un singleton. Donc
\(\color{red}P\color{black}( \color{red}P\color{black}(\emptyset)) = \{\emptyset, \{\emptyset\}\}\)
Produit d'ensembles
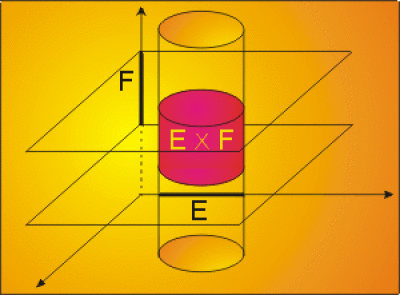
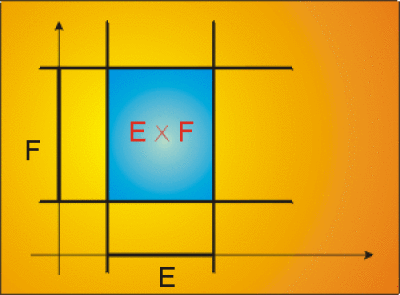
L'ensemble \(\mathbb R ^2,\) représentant les points du plan lorsque l'on a choisi un repère est un ensemble produit ; c'est l'ensemble des couples d'éléments de réels \((x, y),\) \(x\) premier élément du couple, \(y\) deuxième élément du couple. On peut généraliser au produit de deux ensembles \(E\) et \(F\) quelconques :
\(E \times F = \{ (x, y) | x \in E ~et~ y\in F \}\)
Ceci se généralise au produit d'un nombre fini d'ensembles \(E_1, E_2, \dots, E_n\) quelconques :
\(E_1 \times E_2 \times \dots \times E_n = \{ (x_1, x_2, \dots, x_n) | x_1 \in E_1~et~ x_2 \in E_2~ et~ \dots~ et~ x_n \in E_n\}\)