Intersection d'ensembles
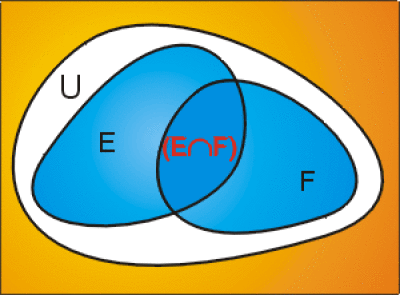
Si \(E\) et \(F\) sont des ensembles, \(E\cap F\) est l'ensemble constitué des éléments qui appartiennent à la fois aux deux ensembles \(E\) et \(F.\)
\(E\cap F = \{x | x\in E~ et~ x\in F \}\)
\(x\in E\cap F\Leftrightarrow (x\in E~ et~ x\in F)\)
On peut à titre d'exercice, démontrer ces propriétés, ainsi que les suivantes.
Lien avec les lois de Morgan
\(x\notin E\cap F\Leftrightarrow (x\notin E~ ou~ x\notin F)\)
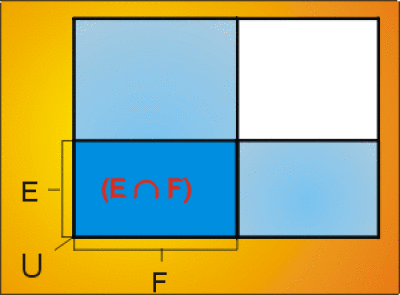
autrement dit:
\(x\notin E\cap F\Leftrightarrow (x\notin E~ et~ x\notin F)~ ou~ (x\notin E~ et~ x\in F)~ ou~ (x\in E~ et~ x\notin F)\)
Propriétés de l'intersection
L'intersection de deux ensembles \(A\) et \(B\) est le plus grand ensemble qui est contenu à la fois dans ces deux ensembles
Ce qui se traduit en langage formalisé par la conjonction de deux propriétés.
\([ A\cap B\subset A ~et~ A\cap B\subset B ]~ et~ [ (C\subset A ~et~ C\subset B)\Leftrightarrow C\subset A\cap B ]\)
Idempotence
Pour tout ensemble \(E,\) on a \(E\cap E = E.\)
\(E\cap F = F\cap E,\) pour tous les ensembles \(E\) et \(F.\)
\((E\cap F)\cap G = E\cap (F\cap G),\) pour tous les ensembles \(E,\) \(F\) et \(G.\) Cela permet de définir l'intersection de trois ensembles, d'un nombre fini d'ensembles.
\(E_1\cap E_2\cap E_3 = \{ x | x\in E_1~ et~ x\in E_2~ et~ x\in E_3 \}\)
\(E_1\cap E_2 \cap\dots\cap E_n = \{ x | x\in E_1 ~et~ x\in E_2 ~et~ \dots ~et~ x\in E_n \}\)
Généralisation
L'intersection se généralise à une intersection quelconque d'une famille d'ensembles indexée par un ensemble non vide \(I.\)
\(\cap_{i\in I}E_i=\{x\in E|\forall i \in I, x\in E_i\}\)
(Le sens du symbole qui veut dire "pour tout" sera revu ensuite.)
Lien avec le connecteur "et"
Supposons l'ensemble \(E\) défini par une propriété \("P"\) et l'ensemble \(F\) défini par une propriété \("Q",\) alors on remarque que l'ensemble \(E\cap F\) est défini par la propriété \("P~ et~ Q"\) :
\(E = \{ x\in U | P(x)\}\)
\(F = \{ x\in U | Q(x)\}\)
\(E\cap F = \{ x\in U | P(x)~ et~ Q(x)\}\)