Complémentaire d'un ensemble
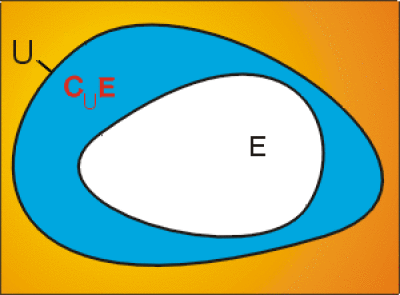
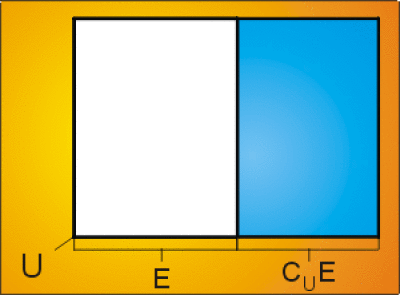
On suppose\( E\subset U.\) On définit un ensemble noté \(C_U E,\) appelé complémentaire de \(E\) dans \(U\) :
\(C_U E = \{x\in U | x\notin E\}\)
\(x\in C_U E\Leftrightarrow (x\in U ~et~ x\notin E)\)
Lien avec le connecteur "non"
Si le sous-ensemble \(E\) de \(U\) est défini par la propriété \("P",\) alors son complémentaire est défini par la propriété \("non~ P".\)
\(E = \{ x \in U | P(x)\}\)
\(C_U E = \{ x\in U | ~non~ P(x) \}\)
Propriété :
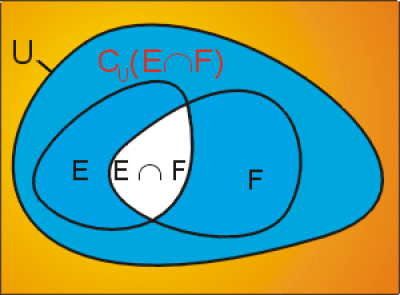
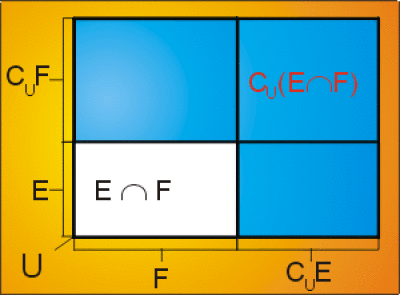
\(E\) et \(F\) sont deux sous-ensembles de \(U.\) En utilisant les lois de Morgan et les autres propriétés logiques, démontrer que :
1. \(C_U (E\cap F) = (C_U E)\cup (C_U F)\)
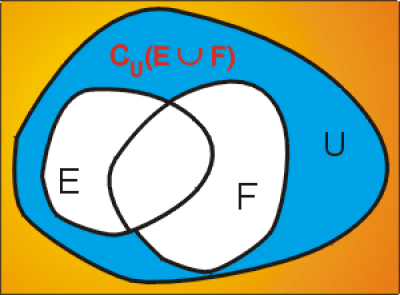
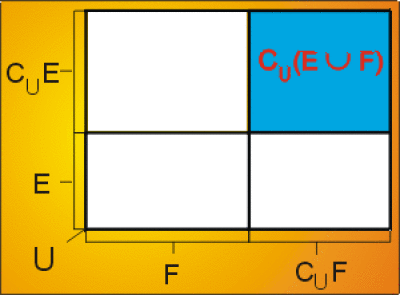
2. \(C_U (E\cup F) = (C_U E )\cap (C_U F)\)
3. \(C_U (C_U E) = E\)
4. \(E\cup (C_U E) = U\)
5. \(E\cap (C_U E) = \emptyset\)
6. \(E\subset F\Leftrightarrow C_U F\subset C_U E\)