Invariances : fil infini (2)
Partie
Question
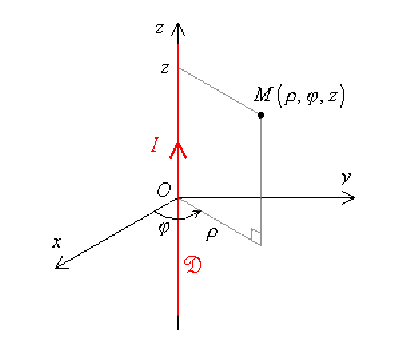
On considère une distribution \(\mathcal{D}\), constituée par un fil rectiligne de longueur infinie parcouru par un courant d'intensité \(I\).
\(\mathcal{D}\) est observée depuis le point \(M\), repéré par ses coordonnées cylindriques \(\rho\), \(\phi\) et \(z\).
Déterminer les déplacements de la distribution qui laissent le système \(\textrm{distribution de courant - point d'observation}\) \((\mathcal{D}, M)\) invariant.
En déduire les coordonnées cylindriques dont dépend le champ magnétostatique \(\vec B\) créé par \(\mathcal{D}\) en \(M\).
Aide simple
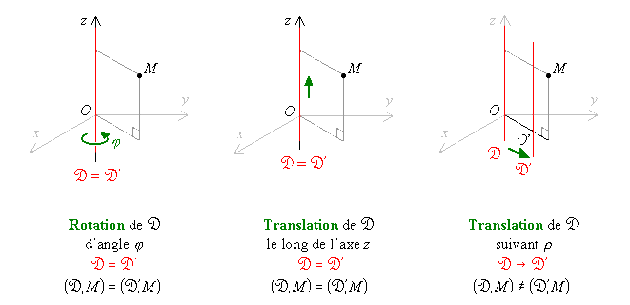
Les déplacements de \(\mathcal{D}\) envisageables dans le repère cylindrique proposé ici sont :
les 2 translations suivant les coordonnées linéaires \(\rho\) et \(z\),
la rotation suivant la coordonnée angulaire \(\phi\).
Solution détaillée
Le système \(\textrm{distribution de courant - point d'observation}\) \((\mathcal{D}, M)\) reste inchangé lors :
de toute rotation de \(\mathcal{D}\) sur elle-même (rotation d'angle \(\phi\)) ; le champ \(\vec B\) créé par la distribution \(\mathcal{D}\) en \(M\) ne dépend donc pas de \(\phi\) ;
de toute translation verticale le long de l'axe \(Oz\) parce que la distribution est de longueur infinie ; le champ \(\vec B\) créé par la distribution \(\mathcal{D}\) en \(M\) ne dépend donc pas de \(z\).
Notons que si on éloigne \(\mathcal{D}\) du point d'observation \(M\) en opérant une translation suivant \(\rho\), alors le système \((\mathcal{D}, M)\) se trouve modifié. Le champ \(\vec B\) créé par la distribution \(\mathcal{D}\) en \(M\) dépend donc de \(\rho\), soit :
\(\vec B(M) = \vec B(\rho)\)
Remarque :
En général, soient \(a_1\), \(a_2\) et \(a_3\) les coordonnées d'un point dans un système de repérage quelconque.
- Si \(a_i\) est une coordonnée axiale ou linéaire (mesurée en distance), alors un déplacement qui modifie \(a_i\) sans modifier les autres coordonnées, est une translation.
- Si \(a_i\) est une coordonnée polaire ou angulaire (mesurée par un angle), alors un déplacement qui modifie \(a_i\) sans modifier les autres coordonnées, est une rotation.